INTRODUCCIÓN

Lasimulación de la activación eléctricamiocárdica mediante modelado por ordenador ha sidoampliamente utilizada en cardiología. En el campo de laelectrofisiología, diversos tipos de modelo han ayudado aentender con mayor profundidad los mecanismos de lasarritmias1,2, las propiedades delautomatismo3, la conducción4,5 y loscircuitos de reentrada6-8. Fenómenos máscomplejos como la actividad fibrilatoria han sido tambiénabordados con estas técnicas9,10, e incluso se haconseguido predecir algunos efectos de los fármacosantiarrítmicos sobre la fibrilaciónventricular11,12 y otras arritmias13,14. Losprincipales modelos de activación utilizados se puedenclasificar en 2 grandes grupos. El primero de ellos se basa en elconcepto de autómata celular, que concibe el tejido como unconjunto de elementos discretos interconectados entre sí.Cada elemento, o autómata, puede adoptar un númerofinito de estados permitidos (p. ej., activo o inactivo), cada unode los cuales cambia en función del estado precedente y delestado de los elementos vecinos de acuerdo con unas reglaspredeterminadas. Las transiciones entre estados individuales rigenla evolución y el comportamiento del sistema en su conjuntoy son deterministas, puesto que bajo las mismas condicionesiniciales, el sistema evoluciona de manera idéntica. Losautómatas celulares son fáciles de programar ypermiten simulaciones rápidas con una carga computacionalmoderada; sin embargo, presentan serias limitaciones al tratar dereproducir varios fenómenos de gran interés enelectrofisiología, como los efectos de la curvatura de losfrentes de activación15. El segundo grupo demodelos, denominados de reacción-difusión, reproducenla dinámica de membrana simulando el paso de las corrientesiónicas a través de los canales iónicos y elpotencial de membrana asociado16-18. La conexiónentre las células se modela mediante resistenciaseléctricas y la propagación del impulso se calcularesolviendo las ecuaciones que gobiernan los circuitoseléctricos19,20. Estos modelos son muchomás realistas y reproducen mejor las situaciones complejas,pero requieren una carga computacional muy elevada y a menudo sonnecesarias muchas horas de cálculo en multiprocesadores parapoder simular 1 o 2 segundos de actividadeléctrica21. El objetivo de este estudio esdiseñar un modelo de activación eléctrica porordenador basado en un autómata celular que permita simularfenómenos electrofisiológicos complejos y que norequiera la carga computacional necesaria en los modelos dereacción-difusión.

MATERIAL YMÉTODO

Diseño del modelo

Eltejido cardíaco se ha modelado como una rejilla de elementosdiscretos, o celdas, que representan grupos de células conun comportamiento intrínseco promedio e interaccionan conlas celdas de su vecindad siguiendo una regla probabilísicade transmisión del impulso eléctrico. Cada celda secomporta como un autómata celular que puede adoptar 3estados: reposo (durante el cual se encuentra relajada yexcitable), refractario 1 (excitada y con capacidad de excitar alas celdas vecinas) y refractario 2 (excitada, pero sin capacidadde excitar a su vecindad). El período refractario 1 semantiene durante una fracción F de la duracióndel potencial de acción (PA), en torno al 10%. Durante elresto del PA, la celda permanece en período refractario 2,para pasar a continuación al valor de reposo, que secorresponde con el intervalo diastólico (ID). Latransición entre estados está regida por 3 leyes:repolarización parcial (transición de refractario 1 arefractario 2), repolarización total (transición derefractario 2 a reposo) y despolarización (transiciónde reposo a refractario 1). Tanto la repolarización parcialcomo la repolarización total tienen lugar de maneradeterminista, conocidos el instante de despolarización y laduración del potencial de acción (DPA). Ladespolarización, por el contrario, está definida entérminos probabilísticos y se basa en 2 factores: porun lado, la excitabilidad de la celda (E), que se incrementacon el tiempo en que aquélla permanece en reposo y, por otrolado, la cantidad de excitación alrededor de cadacélula (Q), de forma que cuanto mayor es estacantidad, mayor es la probabilidad de que el elemento se excite. Sidenotamos por Pjexc a la probabilidadde la celda j de ser excitada, estos 2 factores se combinanen la fórmula:

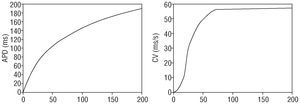
donde i es un elemento de la vecindad, Aies el estado de excitación binario (1 en refractario 1, 0 enotro caso), y dij es la distancia entre loscentros de los elementos i y j. Obsérvese quela fórmula puede aplicarse tanto a sustratos de 2 como de 3dimensiones, extendiendo el sumatorio a los elementos vecinos sobreuna superficie (plana o curva) o a un espacio tridimensional. Laestimación de ambos factores (excitabilidad y cantidad deexcitación) se ha realizado utilizando 2 variablesmacroscópicas --la DPA y la velocidad de conducción(VC)--, teniendo en cuenta las propiedades de restitucióneléctrica del tejido cardíaco. Segúnéstas, la DPA y la VC dependen de la frecuencia deestimulación a la que se encuentra sometido el tejido. Unafrecuencia elevada reduce el ID, condicionando una DPA breve y unaVC baja, mientras que una frecuencia lenta produce elfenómeno contrario. Este comportamiento se recoge en lascurvas de restitución (fig. 1), que han servido para ajustarlos parámetros del modelo.

Fig.1. Curvas de restitución del potencial de acción(izquierda) y de la velocidad de conducción (derecha) enfunción del intervalo diastólico. APD:duración del potencial de acción; CV: velocidad deconducción; DI: intervalo diastólico.

Cálculo de los electrogramas

Para poder calcular los electrogramas (EGM) asociados alpatrón de activación es necesario calcular lacorriente transmembrana a partir del potencial de acción.Para ello se utilizó un potencial de acciónprototipo, obtenido a partir del modelo de Luo y Rudy17,que asocia el tiempo transcurrido en el estado actual de cada celdacon su nivel de voltaje. Asumiendo que el tejido cardíaco sepuede modelar como un medio de dominio único,isotrópico, resistivo y homogéneo, el potencialeléctrico obtenido en un punto cercano a la superficieextracelular se calcula como la suma ponderada de las corrientestransmembrana que se originan en las celdas deltejido22,23. Un EGM unipolar se modela como el registrodel potencial extracelular medido por un electrodo puntual depolaridad positiva, cuya referencia (potencial cero) estásituada en infinito. La distancia del electrodo a la superficiecuantifica la zona de influencia del electrodo, de forma que cuantomás próximo se encuentre al tejido mayor serála captación de campo. Un EGM bipolar se modela como ladiferencia de potencial entre 2 puntos cercanos entre sí, esdecir, como la diferencia entre 2 EGM unipolares.

Elcódigo de simulación y la visualización de losexperimentos realizados se han implementado mediante el paquete desoftware de computación Matlab® (TheMathWorks, Inc.), utilizando un ordenador PC monoprocesador IntelPentium® 4 a 2,19 GHz y con 256 MB deRAM.

RESULTADOS

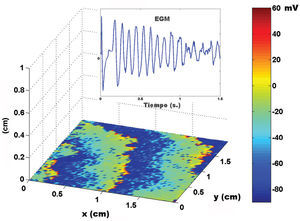
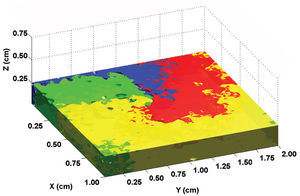
Utilizando como sustrato una lámina bidimensional de80 x 120elementos con propiedades homogéneas, la activacióninicial y simultánea de una línea de elementosgeneró un frente plano de activación con velocidad depropagación uniforme. En la figura 2 se muestran los EGMbipolares y unipolares obtenidos desde distintos puntos delespacio. La estimulación focal sobre el mismo sustratoprodujo un frente circular que se alejaba del punto deestimulación. El EGM monopolar simulado presentó unamorfología QS con el electrodo de registro situado sobre elárea de estimulación, a diferencia de lamorfología rS, obtenida a cierta distancia del centro. Laintroducción en el modelo de áreas inexcitables yzonas de conducción lenta generó circuitos dereentrada estables e inestables. En la figura 3 se muestra lasimulación de un circuito de reentrada en 8, similar a losque se pueden observar en modelos experimentales y en pacientes contaquicardia ventricular sostenida sobre un infarto de miocardiocrónico24-26. Los rectángulos grisesrepresentan áreas de necrosis y el pasillo entre ambas es elárea de conducción lenta. Durante laestimulación desde el extremo izquierdo (figura superior),el electrodo situado sobre el pasillo de conducción lentaregistra un potencial inicial (flecha azul) que corresponde a laactivación del área de conducciónrápida, situada por fuera de las zonas necróticas.Posteriormente se registra un potencial de menor amplitud (flecharoja), tardío y separado del inicial por una líneaisoeléctrica, que corresponde a la activaciónmás lenta del pasillo entre las 2 cicatrices. En pacientescon taquicardias ventriculares e infarto de miocardio se handescrito potenciales similares27. Durante reentrada(fig. 3, inferior) la activación del área deconducción lenta genera un potencial mediodiastólicode amplitud reducida (flecha roja). La concepciónprobabilística de la excitación en nuestro modelo esparticularmente apropiada para simular el comportamiento de losfrentes de activación en zonas con una curvaturapronunciada. El borde convexo del frente encuentra una mayorsuperficie para activar en la dirección de laactivación, por lo que la probabilidad de que se exciten loselementos vecinos en esa dirección disminuye. Dado que lavelocidad de conducción depende esencialmente de eseparámetro, resulta inversamente proporcional a la curvaturadel frente (fig. 4) y reproduce el comportamiento real en estasituación sin necesidad de hipótesis adicionales ad hoc. El modelo permite también efectuar simulacionesde procesos fibrilatorios. Utilizando una lámina depropiedades homogéneas y de 80 x 80 elementos como sustrato,una estimulación rápida con una frecuencia > 8-10Hz genera en pocos segundos curvatura y fragmentaciónirregular de los frentes de onda, típica de laconducción fibrilatoria. En la figura 5 se muestra unejemplo con estimulación a 50 Hz. Obsérvesecómo los EGM obtenidos en las proximidades del sustratoreproducen los obtenidos durante la fibrilación. Finalmente,el modelo permite la simulación del proceso deactivación en 3 dimensiones, dotando de profundidad a larejilla que sustenta el autómata celular. El sustratotridimensional puede definirse con propiedades homogéneas,asumiendo el mismo comportamiento de la ley de activación ensuperficie y en profundidad, pero también puede generarse unmodelo heterogéneo mediante la modificación delcálculo de la distancia en función de ladirección. Este último aspecto permite simularvelocidades de conducción diferentes en sentido transversal,longitudinal y en profundidad, reproduciendo el fenómeno deanisotropía. Al utilizar un sustrato homogéneo, laestimulación sucesiva de un cubo de 80 x 80 x 10 elementos con 2 frentesplanos en dirección perpendicular genera un frente deactivación curvo cuya velocidad de conduccióndisminuye al aproximarse a su centro de rotación. Lacurvatura extrema de la onda de activación la hace girar entorno al núcleo, que permanece inexcitado y conforma de esemodo un rotor similar a los observados durante lafibrilación auricular y ventricular en diversos modelosexperimentales28-30 (fig. 6, vídeo 1 disponibleen el número de enero en:www.revespcardiol.org/).

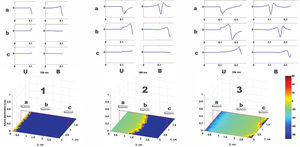
Fig.2. Simulación de un frente de onda plano y loscorrespondientes electrogramas unipolares y bipolares. De izquierdaa derecha se representan 3 momentos de la activación en lalámina de tejido (1: inicio, 2: mitad, 3: final). Lasposiciones del electrodo de registro se representan con las letrasa, b y c. Los electrogramas unipolares (U) y bipolares (B)obtenidos en cada posición se representan en la partesuperior del registro. La barra de la derecha representa el mapa decolores del voltaje de membrana expresado en mV.

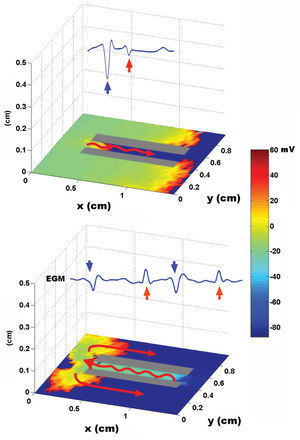
Fig.3. Simulación de un circuito de reentrada en forma de«8». Las flechas rojas dibujadas sobre la láminade tejido representan el sentido de la activación. Laconducción lenta se representa por una flecha ondulada.Sobre cada lámina se muestran los electrogramas bipolaresobtenidos sobre el pasillo entre las áreas de cicatriz(véase texto). El rectángulo de la derecha representael mapa de colores del voltaje de membrana expresado enmV.

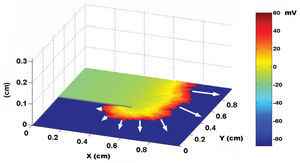
Fig.4. Efecto de la curvatura del frente sobre la velocidad deconducción, representada por las flechas blancas.Obsérvese la disminución de la velocidad al aumentarel grado de curvatura. El mapa de voltaje se representa como en lasfiguras 2 y 3.

Fig.5. Conducción fibrilatoria al estimular el extremoizquierdo de la lámina de tejido con alta frecuencia (50Hz). El recuadro superior muestra el electrograma obtenido alsituar el electrodo sobre la superficie del tejido. Elrectángulo de la derecha representa el mapa de voltaje, comoen las figuras anteriores.

Fig.6. Simul ación de una onda de activación enespiral (rotor). Los diferentes colores representan los tiempos deactivación y el punto central donde se unen corresponde alnúcleo del rotor (véase texto).

DISCUSIÓN

Elmodelo de activación celular descrito es capaz de reproducirmuchos aspectos del comportamiento eléctrico del tejidomiocárdico, incluidos los frentes planos deactivación, los circuitos de reentrada más o menoscomplejos, los efectos de la curvatura del frente, laconducción fibrilatoria y la génesis de rotoresestables, descritos en modelos experimentales de fibrilaciónauricular y ventricular. La simulación de estosfenómenos se consigue con un modelo de autómatascelulares dotado de unas reglas simples, reduciendo así lacarga computacional. El carácter probabilístico de laexcitación es un elemento fundamental en el modelo, ya quereproduce de forma natural el comportamiento de lapropagación en los frentes curvilíneos y permitesimular incluso rotores estables en medios homogéneos de 2 o3 dimensiones.

Sehan publicado distintos modelos de activación ypropagación del impulso cardíaco, que se diferencianen la implementación de la anatomíamacroscópica y microscópica cardíaca y en laaproximación a las propiedades electrofisiológicas dela célula y de las conexiones intercelulares. Algunosmodelos intentan simular la electrofisiología celularmediante la reproducción del comportamiento de lascorrientes iónicas que generan el potencial de accióntransmembrana. Se basan en las ecuaciones originales del modelo depotencial de acción en el axón del calamar gigante deHodgkin y Huxley31 y en sus modificaciones posterioresadaptadas al tejido cardíaco16,17,32-35. Estaaproximación constituye la base de los denominados modelosde reacción-difusión y requiere complejoscálculos matemáticos para describir los procesos deexcitación y propagación del impulso. Con este tipode modelos se ha conseguido reproducir el potencial deacción de las células cardíacas en condicionesnormales y en situaciones patológicas, como la isquemia o lainsuficiencia cardíaca36. Son también muyadecuados para evaluar los efectos electrofisiológicos delos fármacos con acción sobre los canalesiónicos12,37,38. Los efectos de la curvatura enlos frentes simulados con estos modelos son bastante realistas,disminuyendo la velocidad de conducción con el grado decurvatura. La simulación de rotores y de vórticestambién se ha llevado a cabo con estos modelos, tanto en 2como en 3 dimensiones9,15. El principal inconveniente delos modelos de reacción-difusión es que requierentiempos muy prolongados de computación en ordenadores dealta capacidad. Incluso en modelos simplificados39,40,las necesidades de computación son muy elevadas, por lo queson adecuados para simulaciones de pequeñas muestras detejido durante unos pocos segundos. Una ventaja importante denuestro modelo con respecto a los descritos es que suprogramación es más sencilla, requiere mucha menoscarga computacional y puede, por tanto, simular fenómenoscomplejos y/o de duración prolongada sin necesidad de unainfraestructura informática sofisticada. De hecho, nuestraevaluación se ha realizado en ordenadores comerciales defácil disponibilidad, utilizando tiempos razonables parasimulaciones complejas, como las involucradas en losfenómenos fibrilatorios. Con ordenadores de mayor capacidad,como los utilizados actualmente para implementar los modelos dereacción-difusión, se aumentaría de maneraconsiderable la resolución del modelo, consiguiendoresultados más próximos a la preparaciónexperimental y permitiendo, probablemente, la simulación defenómenos en cavidades cardíacas completas con undetalle anatómico realista. El segundo grupo de modelos deactivación se engloba dentro de los denominadosautómatas celulares y se basa en la representacióndel tejido cardíaco como una malla de elementos discretos,que pueden adoptar distintos estados en función de su estadoprecedente y del estado en que se encuentran las celdasvecinas41. En los modelos publicados, lacomunicación entre un elemento y sus vecinos se producesiguiendo una regla determinista, de forma que cada elemento esobligado a cambiar de estado o a permanecer en élsegún sea la situación de las célulascircundantes. Con esta metodología se han podido reproducirbloqueos unidireccionales funcionales con inducción dereentradas estables alrededor de un obstáculo.También se ha conseguido simular ondas espirales que rotanalrededor de un centro fijo, cuya fragmentación se consiguecon la introducción de anisotropía en elsustrato41. Además, la rapidez de cálculoinherente a estos modelos los hacen aplicables a superficies ovolúmenes amplios, simulando el comportamiento de cavidadescardíacas completas. Sin embargo, la reproducción dealgunos fenómenos clave en la dinámica depropagación del estímulo es poco realista o precisala incorporación en el modelo hipótesis adicionalesde difícil justificación. Así ocurre, porejemplo, con la disminución de la velocidad deconducción que se produce al aumentar la frecuencia deestimulación y en especial con el comportamiento de losfrentes curvilíneos, en los que la velocidad deconducción varía inversamente con el grado decurvatura. Este hecho está en la base de muchasobservaciones electrofisiológicas de interés y esdifícilmente reproducible con los modelos al uso. Laintroducción del factor probabilístico en nuestromodelo, según el cual la probabilidad de excitaciónde cada elemento depende del tiempo transcurrido desde suúltima repolarización y del número decélulas activas que hay en la vecindad, reproduce de formanatural ambos fenómenos, sin necesidad de hipótesisadicionales y sin incrementos del tiempo de cálculo. Otrofenómeno que hemos conseguido reproducir de manera directa yque no ha sido comunicado previamente con los modelos deautómatas celulares es la conducción fibrilatoria enel sustrato cuando la frecuencia de estimulación es muyelevada. La posibilidad de obtener EGM virtuales, monopolares ybipolares, en cualquier posición del espacio y con cualquierángulo respecto a la superficie de activación,aumenta la utilidad del modelo y establece una relación conlos registros eléctricos obtenidos directamente en modelosexperimentales o en el laboratorio deelectrofisiología.

Limitaciones

Elmodelo desarrollado se basa en propiedades macroscópicas dela activación, por lo que no tiene en cuenta de formadirecta el comportamiento de los canales y las corrientes celularesiónicas. Por ello, en su estado actual, sería pocoadecuado para simular los efectos de los fármacos o de lasenfermedades genéticas que modifican estas corrientes. Estalimitación, común a todos los modelos deautómatas celulares, podría superarse, al menosparcialmente, introduciendo parámetros que reflejaran demanera indirecta los aspectos más relevantes de ladinámica de canales. En segundo lugar, las simulaciones sehan realizado en un ordenador estándar con baja capacidad decálculo. La utilización de ordenadores máspotentes permitiría una mejor resolución yprobablemente ofrecería un aspecto más realista a lassimulaciones. Además, el modelo se ha evaluado sobre unsustrato virtual sencillo y homogéneo en 2 y 3 dimensiones.La anatomía de las cavidades, la integración deobstáculos anatómicos y la orientación de lasfibras musculares no han sido integradas por el momento.Finalmente, aunque el modelo es capaz de reproducir de una formacualitativa muchos fenómenos interesantes enelectrofisiología básica, no hemos efectuado unavalidación cuantitativa en preparaciones experimentales.Esta validación permitiría un mejor ajuste de losparámetros del modelo y una evaluación de sucapacidad de predicción.

Véaseeditorial en págs. 6-9

Financiado parcialmente con una beca para investigaciónbásica de Guidant España.

Full English text available from: www.revespcardiol.org

Correspondencia: Dr. A. García Alberola.

Pza. del Roble, 36. 30150 La Alberca. Murcia. España.

Correo electrónico: arcadi@secardiologia.es.