El aprendizaje automático (machine learning) en cardiología es cada vez más frecuente en la literatura médica, pero los modelos de aprendizaje automático aún no han producido un cambio generalizado de la práctica clínica. En parte esto se debe a que el lenguaje utilizado para describir el aprendizaje automático procede de la informática y resulta menos familiar a los lectores de revistas clínicas. En esta revisión narrativa se proporcionan, en primer lugar, algunas orientaciones sobre cómo leer las revistas de aprendizaje automático y, a continuación, orientaciones adicionales para quienes se plantean iniciar un estudio utilizando el aprendizaje automático. Por último, se ilustra el estado actual de la técnica con breves resúmenes de 5 artículos que van desde un modelo de aprendizaje automático muy sencillo hasta otros muy sofisticados.
Palabras clave
En esta revisión descriptiva, se considera el aprendizaje automático (AA) (machine learning) o inteligencia artificial (IA) en las publicaciones de cardiología haciendo hincapié en los modelos diagnósticos. En 2022, 1 de cada 60 publicaciones sobre enfermedades cardiovasculares registradas en PubMed incluyeron el AA o la IA como uno de los términos médicos de indexación. A pesar de la abundancia de artículos, son pocos los modelos diagnósticos que se han validado o se han trasladado a la práctica clínica. Aunque es posible que esto no sea peor que lo que ocurre en otras vías de investigación, había una gran expectativa de que la IA revolucionaría la medicina. Así pues, ¿cuándo llegará la revolución?
Al igual que ocurre con muchas de las nuevas tecnologías, el AA en cardiología pasará por el ciclo de sobreexpectación de Garner (en este momento probablemente se encuentre en el «abismo de desilusión» y deberá avanzar hacia la «rampa de consolidación» y la «meseta de productividad»1. Para llegar a estas fases siguientes, es necesario que ocurran 3 cosas. En primer lugar, los clínicos tienen que comprender el lenguaje de la IA y el AA, así como qué se dice y qué no en los artículos que leen. En segundo lugar, los científicos y los clínicos tienen que mejorar los diseños de estudio actuales. En tercer lugar, son necesarios estudios de validación sólidos y una investigación traslacional para identificar dónde y de qué manera el AA hará que la práctica médica cotidiana sea más precisa y productiva.
Este artículo se ha elaborado desde la perspectiva de un científico muy interesado en cómo el AA puede mejorar el diagnóstico. Se centra en los medios diagnósticos, aunque gran parte del contenido es trasladable a otros usos del AA.
En sentido estricto, la IA es una máquina que continúa aprendiendo a través de un flujo de datos que se produce después del desarrollo del modelo inicial. Esto es extremadamente infrecuente. El AA y los modelos estadísticos son los que se elaboran a partir de un conjunto de datos bien delimitado. Casi todos los artículos de cardiología en los que se emplea el término IA son, en sentido estricto, modelos de AA o estadísticos. En esencia, sea cual sea el nombre que demos al método, se trata de intentos de mejorar la predicción o la clasificación2. La aparición del AA y la IA en la literatura médica hace que los clínicos y los investigadores médicos interactúen con la cultura y el lenguaje de la informática incluso mientras el lenguaje de la estadística evoluciona. Es posible que con el paso del tiempo los lenguajes converjan, pero por el momento confunden tanto a quienes leen la literatura especializada como a quienes se mueven entre disciplinas. Para los fines de este artículo, se utilizará un solo término, AA, para englobar todo lo que otros denominan IA, AA o estadística.
La estadística es una disciplina joven (solo han pasado 120 años desde que se presentó el concepto de una hipótesis estadística)3, y la informática es aún más reciente. En los últimos 20 años, la potencia de procesamiento de los ordenadores ha pasado a ser suficiente para que el AA entre en la corriente dominante e impulse la nueva disciplina de la ciencia de datos (una amalgama de informática y estadística). Como ocurre con cualquier nueva disciplina, debemos prever cambios, no solo en el lenguaje, sino también en los conceptos clave. Esto debe motivar precaución en disciplinas que, como la cardiología, usan conceptos de estadística y de informática. Surgen dificultades cuando se transfieren conceptos de una disciplina a otra y pasan a ser axiomáticos. Un ejemplo es el concepto de significación estadística, ubicuo en la medicina, pero que actualmente se considera una mala metodología por los estadísticos académicos4.
El primer apartado del artículo está destinado a todos los que leen artículos médicos. Se comentan las diferencias de lenguaje entre la estadística y la informática que se usan para describir la elaboración de un modelo diagnóstico o una puntuación de riesgo. En el segundo apartado, dirigido a quienes quieren incorporar el AA a su investigación, se introducen otros conceptos adicionales que es necesario tener en cuenta antes de dedicar tiempo y esfuerzo a elaborar nuevos modelos. Por último, se evalúan algunos ejemplos de artículos sobre AA de la literatura cardiológica.
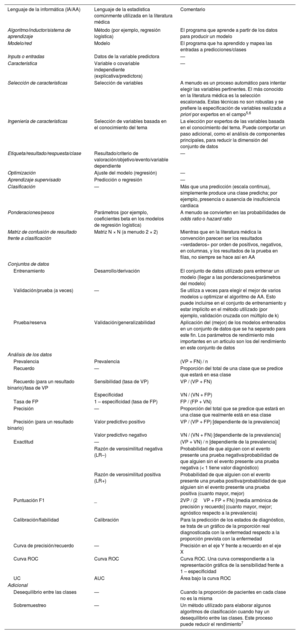
PARTE 1: CÓMO EVALUAR LOS ARTÍCULOS SOBRE APRENDIZAJE AUTOMÁTICOPara comprender un artículo sobre AA, es preciso estar familiarizado con los términos que se emplean. En la tabla 1 se traducen los términos informáticos a términos estadísticos. La tabla no es exhaustiva y hay muchos glosarios de AA disponibles en línea8. Es importante comprender los métodos específicos utilizados, pero también es crucial reconocer la ciencia y la metodología de elaboración de algoritmos de buena calidad, sean cuales sean las técnicas de AA aplicadas.
Términos frecuentes con la «traducción» entre el lenguaje de la informática y el de la estadística
| Lenguaje de la informática (IA/AA) | Lenguaje de la estadística comúnmente utilizada en la literatura médica | Comentario |
|---|---|---|
| Algoritmo/inductor/sistema de aprendizaje | Método (por ejemplo, regresión logística) | El programa que aprende a partir de los datos para producir un modelo |
| Modelo/red | Modelo | El programa que ha aprendido y mapea las entradas a predicciones/clases |
| Inputs o entradas | Datos de la variable predictora | — |
| Característica | Variable o covariable independiente (explicativa/predictora) | — |
| Selección de características | Selección de variables | A menudo es un proceso automático para intentar elegir las variables pertinentes. El más conocido en la literatura médica es la selección escalonada. Estas técnicas no son robustas y se prefiere la especificación de variables realizada a priori por expertos en el campo5,6 |
| Ingeniería de características | Selección de variables basada en el conocimiento del tema | La elección por expertos de las variables basada en el conocimiento del tema. Puede comportar un paso adicional, como el análisis de componentes principales, para reducir la dimensión del conjunto de datos |
| Etiqueta/resultado/respuesta/clase | Resultado/criterio de valoración/objetivo/evento/variable dependiente | — |
| Optimización | Ajuste del modelo (regresión) | — |
| Aprendizaje supervisado | Predicción o regresión | — |
| Clasificación | — | Más que una predicción (escala continua), simplemente produce una clase predicha; por ejemplo, presencia o ausencia de insuficiencia cardiaca |
| Ponderaciones/pesos | Parámetros (por ejemplo, coeficientes beta en los modelos de regresión logística) | A menudo se convierten en las probabilidades de odds ratio o hazard ratio |
| Matriz de confusión de resultado frente a clasificación | Matriz N × N (a menudo 2 × 2) | Mientras que en la literatura médica la convención parecen ser los resultados «verdaderos» por orden de positivos, negativos, en columnas, y los resultados de la prueba en filas, no siempre se hace así en AA |
| Conjuntos de datos | ||
| Entrenamiento | Desarrollo/derivación | El conjunto de datos utilizado para entrenar un modelo (llegar a las ponderaciones/parámetros del modelo) |
| Validación/prueba (a veces) | — | Se utiliza a veces para elegir el mejor de varios modelos u optimizar el algoritmo de AA. Esto puede incluirse en el conjunto de entrenamiento y estar implícito en el método utilizado (por ejemplo, validación cruzada con múltiplo de k) |
| Prueba/reserva | Validación/generalizabilidad | Aplicación del (mejor) de los modelos entrenados en un conjunto de datos que se ha separado para este fin. Los parámetros de rendimiento más importantes en un artículo son los del rendimiento en este conjunto de datos |
| Análisis de los datos | ||
| Prevalencia | Prevalencia | (VP + FN) / n |
| Recuerdo | — | Proporción del total de una clase que se predice que estará en esa clase |
| Recuerdo (para un resultado binario)/tasa de VP | Sensibilidad (tasa de VP) | VP / (VP + FN) |
| Especificidad | VN / (VN + FP) | |
| Tasa de FP | 1 – especificidad (tasa de FP) | FP / (FP + VN) |
| Precisión | — | Proporción del total que se predice que estará en una clase que realmente está en esa clase |
| Precisión (para un resultado binario) | Valor predictivo positivo | VP / (VP + FP) [dependiente de la prevalencia] |
| Valor predictivo negativo | VN / (VN + FN) [dependiente de la prevalencia] | |
| Exactitud | — | (VP + VN) / n [dependiente de la prevalencia] |
| Razón de verosimilitud negativa (LR–) | Probabilidad de que alguien con el evento presente una prueba negativa/probabilidad de que alguien sin el evento presente una prueba negativa (< 1 tiene valor diagnóstico) | |
| Razón de verosimilitud positiva (LR+) | Probabilidad de que alguien con el evento presente una prueba positiva/probabilidad de que alguien sin el evento presente una prueba positiva (cuanto mayor, mejor) | |
| Puntuación F1 | _ | 2VP / (2VP + FP + FN) [media armónica de precisión y recuerdo] (cuanto mayor, mejor; agnóstico respecto a la prevalencia) |
| Calibración/fiabilidad | Calibración | Para la predicción de los estados de diagnóstico, se trata de un gráfico de la proporción real diagnosticada con la enfermedad respecto a la proporción prevista con la enfermedad |
| Curva de precisión/recuerdo | — | Precisión en el eje Y frente a recuerdo en el eje X |
| Curva ROC | Curva ROC | Curva ROC. Una curva correspondiente a la representación gráfica de la sensibilidad frente a 1 – especificidad |
| UC | AUC | Área bajo la curva ROC |
| Adicional | ||
| Desequilibrio entre las clases | — | Cuando la proporción de pacientes en cada clase no es la misma |
| Sobremuestreo | — | Un método utilizado para elaborar algunos algoritmos de clasificación cuando hay un desequilibrio entre las clases. Este proceso puede reducir el rendimiento7 |
AUC: área bajo la curva; FN: falso negativo; FP: falso positivo; n: suma de VP, VN, FP, FN; curva ROC: curva de características operativas del receptor; VN: verdadero negativo; VP: verdadero positivo.
Los artículos sobre AA pueden agruparse en 3 categorías: identificación de asociaciones entre las variables introducidas y un criterio de valoración, u objetivo, ilustración del potencial de una técnica y elaboración de un modelo para modificar la práctica. En ocasiones, los artículos combinan estos objetivos. En un artículo se puede afirmar que se elabora un modelo diagnóstico, pero se pueden comentar también relaciones causales, aunque estas no son necesarias para que el modelo resulte útil clínicamente. A menudo no se intenta mostrar que el modelo elaborado es mejor que los modelos actualmente existentes. Esto no invalida el estudio, pero se debe reconocer que el modelo se encuentra en una fase inicial de elaboración y aún no está listo para su aplicación.
P2: ¿Cuál es la cohorte, de dónde proceden los datos?Si la población del estudio no refleja la población a la que se va a aplicar el modelo, es posible que el algoritmo tenga un sesgo. Esto se denomina sesgo de espectro (véase un ejemplo en cardiología en Tseng et al.9). El lector debe prestar especial atención a cómo se han abordado la raza, la edad y el origen étnico. Por ejemplo, la puntuación de riesgo de mortalidad en pacientes con cardiopatía de la American Heart Association asigna un riesgo inferior a los pacientes negros10, lo cual puede conducir a una menor intervención, lo que puede comportar desigualdades sistemáticas arraigadas en la sociedad y los sistemas de asistencia sanitaria.
P3: ¿Cuál es el criterio de valoración?Al evaluar la utilidad de un modelo, es importante tener en cuenta si pronostica algo que tenga trascendencia clínica y si el resultado empleado como criterio de valoración podrá afectar a las decisiones de tratamiento o de estudio diagnóstico. Además, es preciso considerar si el modelo diagnostica algo que, de otro modo, sería difícil de diagnosticar en el momento en que se prevé aplicarlo. Estas son las preguntas importantes del «¿y qué?».
Por otra parte, se debe tener en cuenta si el modelo clasifica (asigna una clase, por ejemplo, si un paciente presenta insuficiencia cardiaca o no) o proporciona una probabilidad de que un paciente se encuentre en una determinada clase (p. ej., un paciente tiene una probabilidad del 31,4% de tener insuficiencia cardiaca). Una predicción puede convertirse luego en una clasificación mediante la aplicación de un umbral. Un árbol de decisión es un ejemplo de método de clasificación, y una regresión logística es un método capaz de proporcionar probabilidades. La literatura sobre AA no siempre diferencia los 2 tipos y, por ejemplo, puede llamar regresión logística a un método de clasificación aplicando un umbral (a menudo, una probabilidad arbitraria del 50%).
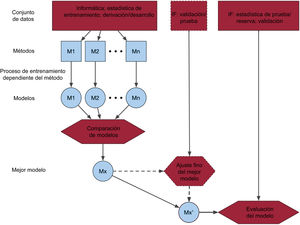
P4: ¿Cuál es el método de aprendizaje automático utilizado y por qué?A menudo la elección del método de AA es arbitraria y no está justificada. Es posible que los éxitos recientes de métodos empleados para problemas similares sean la razón de que se elija un método concreto. Cuando se consideran varios métodos, puede emplearse un proceso que utiliza un conjunto de datos de desarrollo o entrenamiento o uno de prueba para crear el mejor modelo de AA (figura 1). El proceso exacto puede variar, y el lector encontrará descripciones que pueden ser bastante complejas y quedan relegadas a un suplemento, como las de la selección de variables, la validación cruzada (múltiplo de K, dejar uno fuera [leave-one-out] y remuestreo [bootstrapping]) y el ajuste hiperparamétrico para el control del proceso de aprendizaje. Una dificultad con la que puede encontrarse un lector clínico es no saber en qué medida se ha revisado un artículo desde la perspectiva metodológica informática (o estadística). Los editores podrían ayudar a aclararlo indicando los tipos de revisores del artículo.
Figura central. Representación esquemática del proceso de desarrollo y validación de un modelo de aprendizaje automático. Se entrenan/derivan y comparan uno o varios modelos utilizando métodos diferentes. El mejor modelo, Mx, después puede ser objeto de una validación adicional o un ajuste fino de los parámetros. El modelo final se valida en un conjunto de datos, que puede ser externo (de otras fuentes), corresponder a un periodo temporal diferente del de otro u otros conjuntos de datos o elegirse de manera aleatoria a partir de la misma fuente de datos que el otro u otros conjuntos de datos. IF: informática; M1: modelo 1; M2: modelo 2; Mn: modelo n.
Los parámetros de medición cruciales para evaluar el AA son los de la cohorte de validación con la elección del «mejor» modelo. El lector puede encontrar también los parámetros de medición utilizados para comparar modelos, alguno de los cuales se comenta en el siguiente apartado, destinado a quienes desarrollan modelos.
Parámetros de medición diagnósticosPara la clasificación diagnóstica y del riesgo, los parámetros de medición más comúnmente utilizados son la representación gráfica de la curva de características operativas del receptor (ROC) y su correspondiente área bajo la curva (AUC) ROC. Sin embargo, no deben emplearse solas o sin una ulterior interpretación.
El gráfico ROC es una curva creada con la evaluación del rendimiento diagnóstico en todos los umbrales posibles del criterio de valoración (probabilidades para el AA). Se calculan la sensibilidad y la especificidad en cada umbral. El gráfico ROC es la curva formada por la sensibilidad frente a 1 – especificidad, y el AUC es el área bajo esta curva. A menudo se parte del supuesto de que la diagonal principal corresponde a lo que se obtendría al hacerlo a cara o cruz y de que solo son útiles los valores de la curva situados por encima de la diagonal. Pero esto es incorrecto11. Solo el punto central de la diagonal (0,5, 0,5) es equivalente a lanzar una moneda al aire. Otros puntos pueden contener una información útil desde el punto de vista diagnóstico, dependiendo de cuál sea la prevalencia. Por ejemplo, el punto 0,0 situado en el extremo inferior izquierdo equivale a afirmar que todos los resultados de la prueba diagnóstica son negativos, lo cual, en una población con baja prevalencia, tiene un probabilidad muy superior a 0,5 (igual a 1 – prevalencia).
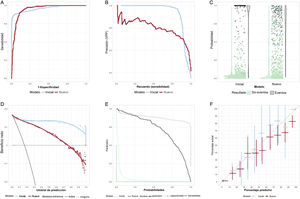
El AUC puede interpretarse como la probabilidad de que, si se extraen aleatoriamente los resultados del modelo para un paciente que ha presentado el resultado de interés y para otro que no lo ha presentado, el primero tenga un valor de salida mayor que el del segundo. Teniendo esto en cuenta, resulta difícil comprender por qué el AUC ha pasado a ser un parámetro de medición tan popular para describir el rendimiento de un modelo. En la figura 2A se muestra cómo 2 modelos con valores de AUC idénticos (0,94) pueden tener curvas ROC diferentes. En una situación clínica en que es muy grande el coste de pasar por alto un diagnóstico, la curva con la mayor sensibilidad a una especificidad alta sería el modelo preferido.
A: curvas de características operativas del receptor (ROC) de 2 modelos con un área bajo la curva ROC idéntica. B: curva de precisión-recuerdo; el modelo inicial es el mejor a la precisión máxima, pero para un recuerdo> 0,92, el modelo nuevo es el que tiene la mejor precisión. C: gráficos de dispersión de puntos y de violín; la barra en el gráfico de violín indica la mediana de probabilidad para el modelo; como alternativa, puede usarse un gráfico de cajas y bigotes. D: curva de decisión/curva de beneficio neto; mejor cuanto mayor sea el beneficio neto; en general ilustra solo por encima de los umbrales de predicción de la trascendencia clínica; en este caso, el modelo inicial es mejor que el modelo nuevo, excepto a probabilidades bajas (< 0,15). E: gráfico de evaluación del riesgo; cuanto más próximas al extremo inferior izquierdo están las curvas verde azulado, mejor es el modelo para asignar probabilidades bajas a quienes no presentan el resultado y cuanto más próximas al extremo superior derecho están las curvas negras, mejor es el modelo para asignar probabilidades altas a quienes presentan el resultado; en este caso, el modelo nuevo mejora el modelo basal para quienes no presentan el resultado, pero para probabilidades> 0,2, es peor que el modelo inicial. F: gráfico de calibración; lo ideal es que todos los puntos se sitúen en la línea diagonal, lo cual indica que el riesgo predicho refleja con exactitud el riesgo actual; se muestran los intervalos de confianza del 95%.
En la figura 2 se muestran algunos gráficos diagnósticos menos frecuentes que pueden aparecer en la literatura médica. La precisión/recuerdo (valor predictivo positivo [VPP] / sensibilidad) es de uso frecuente en informática. Puede utilizarse para elegir entre distintos modelos a los valores deseados de VPP o de sensibilidad (figura 2B). La figura 2C es un gráfico de violín. En este caso muestra que el modelo de la situación inicial tiene unas probabilidades muy altas para quienes tienen el evento. La curva de beneficio neto (curva de decisión) de la figura 2D muestra que, para una situación en que los falsos negativos y los falsos positivos tienen una ponderación equilibrada, hay un beneficio neto de utilizar el nuevo modelo solo cuando se aplica un umbral de predicción <0,1. El gráfico de evaluación del riesgo (figura 2E) muestra que la diferencia de rendimiento entre el modelo inicial y el modelo nuevo es consecuencia de una pequeña mejora en la reducción de la probabilidad de quienes no presentan el evento (la curva continua de color verde azulado, «1 – especificidad», para el modelo nuevo se aproxima al extremo inferior izquierdo en comparación con la curva punteada del modelo inicial), pero hay una reducción notable e inapropiada de la probabilidad para quienes tienen el evento (la curva continua de sensibilidad se desplaza hacia el extremo inferior izquierdo para el modelo nuevo, en vez de hacia el extremo superior derecho, en comparación con el modelo inicial).
Algunos modelos de AA presentan la exactitud, la proporción de verdaderos positivos y verdaderos negativos en la cohorte, pero esta no es una medida útil en las situaciones clínicas habituales de baja prevalencia. Por ejemplo, se podría estar a la puerta de un hospital y rechazar a todos los que tuvieran dolor torácico. Es probable que la exactitud para el diagnóstico del infarto de miocardio sea ≥ 90%. Por desgracia, la sensibilidad es del 0% y uno se quedaría sin trabajo, iría a la cárcel o algo peor.
Para los modelos clasificatorios, los parámetros de medición frecuentes son la sensibilidad, el valor predictivo negativo (VPN), la especificidad y el VPP (tabla 1). Para generar estos parámetros, es importante elegir, mediante un consenso entre los clínicos, umbrales que permitan una interpretación clínica12. Cuando hay diferencias de prevalencia entre los conjuntos de datos de desarrollo, de prueba y de validación, no deben compararse el VPN ni el VPP, ya que varían con la prevalencia. Estos parámetros pueden acompañarse de las razones de verosimilitud (likelihood ratios) negativa y positiva (LR–, LR+), que son parámetros poco sensibles a la prevalencia. Estos parámetros indican si la prueba aporta algún valor diagnóstico adicional. Los científicos de datos pueden presentar también la puntuación F1.
Todos los parámetros deben presentarse junto con un intervalo de confianza y es importante tener en cuenta ambos límites al interpretar los resultados13. La estimación puntual es solo uno de los muchos valores posibles que podrían darse en la población subyacente. El valor nulo puede estar dentro del intervalo de confianza pero, contrariamente a lo que con frecuencia se afirma, esto no significa que la prueba no sea útil. Por ejemplo, si la LR– (intervalo de confianza del 95%) es de 0,80 (0,55-1,05), y si una LR– <0,9 se considera clínicamente trascendente, en este caso los valores de 0,6 a 0,9 son todos más probables que el valor nulo. Para los algoritmos diagnósticos, uno de los límites puede ser importante desde una perspectiva de seguridad o utilidad; por ejemplo, el límite inferior de la sensibilidad es de gran importancia para evaluar la seguridad.
Importancia de la calibraciónLa calibración es importante, aunque a menudo no se presenta en el análisis14. Las pruebas de bondad de ajuste (p. ej., la prueba de Hosmer-Lemonshow) son mucho menos informativas que un gráfico de calibración de la proporción real de personas con el criterio de valoración frente a la parte predicha con ese criterio (figura 2F). Los modelos que discriminan pueden tener una mala calibración, lo que limita su utilidad. Deben verificarse las curvas de calibración a las probabilidades de interés. Por ejemplo, cuando la tasa predicha es del 3% pero la tasa real es del 6%, esto podría conducir a una subestimación del riesgo con trascendencia clínica en una proporción muy grande de las personas a las que se aplique.
P6: ¿Cómo se abordan el sesgo y la equidad?Además de valorar cómo ha abordado el artículo el posible sesgo de espectro, hay que considerar si se presenta evidencia sobre el rendimiento del modelo en subgrupos específicos con conocida inequidad de población. Por ejemplo, ¿se presentan parámetros del rendimiento para una población indígena? Al examinar estos datos, hay que tener presente que los intervalos de confianza serán más amplios cuando las cifras sean bajas y tener cuidado de no interpretar que el modelo «no funciona» en grupos de población específicos por este motivo.
Lecturas recomendadasEntre los artículos útiles para comprender el AA, se encuentran los de Marteen van Smeden15, Sebastian Vollmer del Alan Turing Institute16 y el experto en AA de Google Alphabet Yun Liu17. Van Smeeden et al. abordan la pregunta «¿Es realmente necesario un nuevo modelo de predicción?». La primera pregunta de Vollmer se refiere al beneficio para el paciente. Cuando los investigadores no han sido «conscientes del camino desde el desarrollo hasta la aplicación», es posible que el artículo no supere la prueba del «¿y qué?». En el artículo de Yun Liu sobre cómo leer artículos de AA, los autores afirman que «la gestalt clínica desempeña un papel crucial a la hora de evaluar si los resultados son creíbles o no: dado que uno de los principales puntos fuertes de los modelos de AA es la uniformidad y la ausencia de fatiga, una verificación cuidadosa de los resultados de AA creíbles es que un experto experimentado podría reproducir la exactitud que se le atribuye si dispusiera de mucho tiempo». Por último, si se desea un instrumento formal para evaluar el riesgo de sesgo en un modelo de predicción, propongo utilizar la herramienta PROBAST18,19.
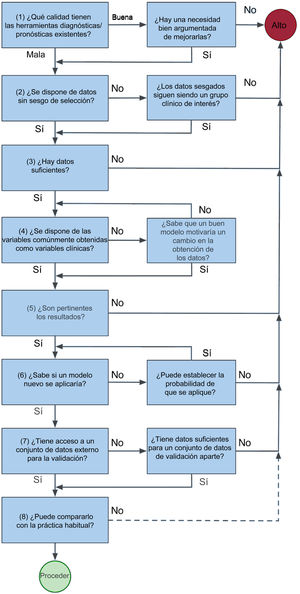
PARTE 2: CÓMO LLEVAR A CABO UNA INVESTIGACIÓN CON APRENDIZAJE AUTOMÁTICOLa figura 3, de tipo heurístico, es una breve guía para llevar a una decisión sobre la viabilidad de un estudio.
Antes de desarrollar un nuevo modelo, evalúe la calidad de las herramientas ya existentes y determine si permiten responder a su pregunta de investigación, y luego evalúe la disponibilidad de datos pertinentes. Para superar la prueba del «¿y qué?», pregunte a quienes pueden verse más afectados por la introducción de una nueva herramienta, incluidos los pacientes, el personal clínico y la administración del sistema sanitario. Adopte, por ejemplo, los principios del «codiseño». Con ellos se avanza un paso más que con la consulta y se asegura que quienes se vayan a ver más afectados reciban un «producto» que tenga sentido para ellos. Por ejemplo, en Nueva Zelanda se utiliza el codiseño para reducir las inequidades que sufren los maoríes en la prestación de atención a la salud cardiaca. Al acudir primero a las comunidades maoríes con una agenda muy limitada, el investigador reconoce la primacía de la comunidad y el individuo para tomar decisiones sobre su propia salud. La investigación puede averiguar, por ejemplo, que la comunidad tiene poco interés en las probabilidades del modelo propuesto, pero que propone algo diferente en su lugar. Es de destacar que el «Plan para una Carta de Derechos en cuanto a la Inteligencia Artificial» de Estados Unidos adopta un enfoque similar en su primer principio, que establece que «Los sistemas automatizados deben desarrollarse consultando a diversas comunidades, partes interesadas y expertos en la materia para determinar las preocupaciones, los riesgos y las posibles repercusiones del sistema»20.
Evalúe la idoneidad de los datos disponibles. Los conjuntos de datos grandes, obtenidos de manera sistemática, pueden tener limitaciones, como la falta de material clínicamente relevante o los datos de resultados clínicos sesgados debido a que se usan principalmente para finalidades económicas. Para evitar el sesgo de selección, considere el grupo de pacientes destinatarios y evalúe el sesgo de los posibles conjuntos de datos. Si los datos excluyen a determinados grupos de pacientes, el modelo desarrollado tendrá limitaciones en cuanto a su pertinencia y es posible que haya un sesgo del tratamiento en contra de esos grupos, sobre todo si son grupos en mayor riesgo. Por ejemplo, un modelo de predicción de la insuficiencia cardiaca desarrollado principalmente en una población no maorí puede subestimar la predicción de eventos en los maoríes, con lo que se perpetúan las inequidades.
Para establecer qué cantidad de datos es suficiente, se han popularizado reglas empíricas de (un mínimo de) 10 a 20 eventos del criterio de valoración por variable, pero el reciente trabajo de Richard Riley proporciona instrumentos para cálculos a priori que fundamenten el número máximo de variables en un modelo21–23. Si faltan algunos datos de las variables, se acepta la imputación como opción preferible a descartar a los pacientes con datos incompletos, ya que reduce el riesgo de sesgo y las incertidumbres en las estimaciones finales. Sin embargo, es necesario evaluar primero si los datos faltan de una manera aleatoria24–28.
Los métodos de selección escalonada de las variables, que utilizan umbrales arbitrarios del valor de p para reducir el número de variables, son ya obsoletos y pueden dar lugar a modelos sesgados y poco transferibles5,6. El punto de partida para la selección de las variables consiste en consultar a expertos para determinar los factores predictivos comúnmente registrados en la práctica clínica29. Si el modelo se basa en variables a las que solo puede accederse en retrospectiva, es necesario tener una razón sólida para su inclusión, ya que requeriría también su obtención prospectiva para el uso futuro del modelo.
En el pasado, tal vez por la necesidad de utilizar algoritmos sencillos que pudieran aplicarse a la cabecera del paciente, las variables continuas como la edad o la presión arterial sistólica se dicotomizaban. Este proceso desecha información y es innecesario con la tecnología actual30.
Los resultados utilizados en el modelo deben ser de interés para los usuarios del modelo. Por ejemplo, si el objetivo es desarrollar un modelo de predicción hospitalaria para los cardiólogos, ¿es pertinente para los cardiólogos y qué grado de mejora sería útil respecto a las predicciones actuales?
Modificar la práctica clínica es difícil, pero es el objetivo implícito de todo AA. Antes de emprender una investigación con AA, establezca la necesidad del modelo y los obstáculos existentes para su aplicación. Entre ellos pueden estar el carácter de «caja negra» de algunos AA, las prioridades de gestión y los recursos de tecnologías de la información. El codiseño puede ser útil para superar estos obstáculos.
No es estrictamente necesario un conjunto de datos de valoración externa y hay buenas técnicas de validación interna que siempre deben aplicarse. La mejor práctica consiste en evitar la división del conjunto de datos en subconjuntos más pequeños31,32. Sin embargo, la mejor forma de evaluar la generalización continúa siendo el uso de conjuntos de datos externos. Se deben identificar antes del desarrollo del modelo y se elegirá el conjunto de datos más grande como conjunto para el desarrollo del modelo.
Por último, si se pretende que sea algo más que un ejercicio académico, debe compararse con la práctica clínica habitual. Aunque no hacerlo no tiene consecuencias fatales, ciertamente implica que sea mucho más probable que un modelo sea adoptado por otros.
Elección de algoritmosAunque el diagnóstico comporta una clasificación, los modelos de AA no tienen por qué tener como resultado una clasificación. Un modelo que produzca un resultado de probabilidad puede ser más informativo. La regresión logística puede entenderse como un algoritmo inicial que es fácil de aplicar e interpretar. Los modelos de conjuntos (ensemble models), como los bosques aleatorios (random forests) o la potenciación del gradiente (gradient boosting), pueden mejorar lo que aporta una regresión logística simple. Esta es la conocida sabiduría popular. Existen varias formas de modelos de conjunto que combinan múltiples modelos o usan un remuestreo (bootstrapping). Puede consultarse un examen reciente de estos métodos en Sagi y Rokach33.
Presentación de resultadosEs importante indicar cómo se ha elegido el «mejor» modelo para la validación y esta metodología debe especificarse a priori. No es necesario que se base en el AUC. Tal como se muestra en la figura 1, hay otras consideraciones en función de la finalidad que tenga el modelo. Esto incluye la calibración. Los parámetros de medición que deben considerarse son, entre otros, el logaritmo de verosimilitud, la habilidad de Brier (Brier skill) (el cambio relativo de la puntuación de Brier respecto al modelo inicial), la R2 de Nagelkerk y la mejora de discriminación integrada presentadas por separado para las personas con y sin eventos. Si el uso que se pretende darle no incluye la presentación de probabilidades predichas, el mejor modelo puede ser el que tenga la máxima especificidad para una sensibilidad mínima preespecificada (para identificar a los pacientes en bajo riesgo) o viceversa (para identificar a los pacientes en alto riesgo).
Las principales medidas del resultado son la discriminación (predefinida) y la calibración en la cohorte de validación del mejor modelo. Deben indicarse en el resumen junto con un intervalo de confianza.
PARTE 3: EJEMPLOS DE APRENDIZAJE AUTOMÁTICO EN CARDIOLOGÍAApoyo para la decisión respecto al infarto de miocardio en el servicio de urgenciasLa troponina es el más potente factor predictivo de un infarto de miocardio (lo cual no es de extrañar, puesto que forma parte de la propia definición) en el momento de la presentación inicial en el servicio de urgencias. Las concentraciones de troponina se asocian también con la edad y el sexo, y estos 2 parámetros se asocian también con el infarto de miocardio. La cinética de la troponina de alta sensibilidad y, en particular, la rapidez de cambio también están relacionadas con los resultados34.
Las herramientas de apoyo a la decisión para la estratificación del riesgo en el servicio de urgencias se han creado a partir de la opinión experta de una persona (HEART), han utilizado puntuaciones desarrolladas para otros fines (ADAPT), han desarrollado una puntuación específica para ese fin mediante regresión logística (EDACS) y han usado árboles de decisión simples basados en una sola variable, el resultado de la troponina35–39. La aplicación de un AA que puede proporcionar apoyo con probabilidades predichas es nueva. En 2017, el T-MACS de Body et al.40 combinó la troponina de alta sensibilidad con el electrocardiograma, la naturaleza del dolor, los vómitos y la sudoración en una regresión logística y proporciona una probabilidad de infarto de miocardio. La discriminación fue alta (0,90 en el conjunto de datos de validación externa) y un umbral elegido para facilitar la toma de decisiones hacía que el modelo pudiera aplicarse clínicamente con alto grado de seguridad (sensibilidad muy alta). El rendimiento obtenido con el umbral fue bueno y el modelo se ha aplicado en la región metropolitana de Manchester, en Reino Unido41. No se presentó una calibración, y el algoritmo no estuvo bien calibrado en una validación externa adicional42. Esto indica la necesidad de recalibración antes de aplicarla a un nuevo contexto.
Than et al.43 evaluaron un modelo de AA en un amplio conjunto de datos internacionales, desarrollado por la unidad de medios diagnósticos de Abbott, en el que se utilizó un conjunto de variables muy sencillo: edad, sexo, 2 determinaciones de troponina y tiempo entre las 2 determinaciones. El modelo se había desarrollado empleando una potenciación de gradiente, tenía una discriminación alta y estuvo bien calibrado en el conjunto de datos de calibración. No se comparó con otros modelos. En una validación externa adicional, la discriminación seguía siendo alta y los parámetros del rendimiento con el umbral, buenos44. Sin embargo, el modelo produjo una infrapredicción del infarto de miocardio en valores de predicción < 50%. Esto señala nuevamente la importancia de verificar la calibración en cada cohorte a la que probablemente se aplique un modelo.
Diagnóstico de la insuficiencia cardiacaSe han desarrollado modelos de AA para el diagnóstico de la insuficiencia cardiaca que se han resumido en 2 revisiones sistemáticas45,46. Dichas revisiones resaltan la diversidad de las 2 situaciones en que se cree que el AA resulta útil, así como las técnicas empleadas. Por ejemplo, se usan redes neuronales convolucionales para potenciar la interpretación de las imágenes de biopsia de toda una preparación47, diversos métodos predicen el reingreso, aunque con poca discriminación48, y las redes neuronales profundas usaron parámetros demográficos y electrocardiográficos para identificar la insuficiencia cardiaca, con una buena discriminación, pero no se realizó ninguna comparación con métodos actuales49.
Dos notables artículos de cardiología con AA muestran las características del desarrollo y la evaluación de un modelo de calidad. El primero, de Dana Sax et al.50, tuvo como objetivo mejorar la predicción de eventos adversos a 30 días en pacientes que acuden a servicios de urgencias por una insuficiencia cardiaca aguda. Estos autores compararon un instrumento ya existente, STRATIFY, con su modelo de AA elaborado con 13 variables propias de STRATIFY y otras 58 posibles variables adicionales. Los datos se dividieron en un conjunto de datos de prueba (20%) y otro de desarrollo (80%), y se utilizó una imputación simple para los datos no disponibles de variables y una validación cruzada de 10 veces para el ajuste hiperparamétrico. La evaluación del modelo se realizó, en general, mediante el AUC, la ROC y las curvas de calibración. Se presentaron también las curvas de precisión/recuerdo y, para los umbrales de riesgo especificados a priori, la sensibilidad, la especificidad, la razón de verosimilitud negativa y positiva, el VPN, el VPP y la puntuación F1. Para todos los umbrales se utilizó la reclasificación neta para comparar un modelo de regresión logística con un modelo XGBoost. Los autores comentaron detalladamente las limitaciones, incluido el posible sesgo derivado de su naturaleza retrospectiva, y los planes futuros con vistas a la aplicación. Se demostró una mejora con un modelo de AA respecto a STRATIFY (AUC, 0,76 frente a 0,68). Aunque utilizar solamente el AUC para la comparación global es limitante y un AUC de 0,76 puede no ser suficiente para provocar un cambio en la práctica clínica, la evaluación detallada del rendimiento con los umbrales clínicamente pertinentes atenuó esta limitación. La otra limitación es que no hay una evaluación del rendimiento en relación con características demográficas clave.
El segundo, de Kuan Lee.51, utilizó datos de investigación de 14 estudios y 13 países con validación (adjudicación) de los resultados para desarrollar y validar un modelo de apoyo a la decisión para el diagnóstico de la insuficiencia cardiaca. Los conjuntos de datos se identificaron mediante una metodología de revisión sistemática que incluyó la evaluación del riesgo de sesgo. Se desarrollaron 4 modelos de AA empleando conjuntos de datos con imputación múltiple. La validación comportó el tratamiento de cada uno de los 14 conjuntos de datos como conjuntos de datos externos (sin imputación) y utilizar los demás conjuntos de datos para el desarrollo del modelo. Para valorar el rendimiento del modelo se utilizaron varios criterios, como la calibración, la puntuación de Brier, el AUC y las proporciones de pacientes situados por encima y por debajo de los criterios de probabilidad especificados. Se elaboraron también curvas de decisión (incluidas en el suplemento). Se evaluó el rendimiento diagnóstico para una amplia variedad de subgrupos demográficos. Se abordaron bien las limitaciones del estudio, en especial al reconocer la posibilidad de un sesgo de selección, ya que 16 de los 30 estudios aptos para la inclusión no participaron. Este es otro estudio excelente, con pocos puntos débiles. Uno de ellos —el uso del VPN y el VPP en vez de la sensibilidad y la especificidad para comparar subgrupos de pacientes— debe evitarse, ya que las diferencias en estos parámetros pueden deberse a diferencias de prevalencia de insuficiencia cardiaca en cada subgrupo, en vez de a diferencias reales en el rendimiento del modelo.
Probabilidad de enfermedad coronariaForrest et al.52 desarrollaron un AA a partir de registros de salud electrónicos para utilizarlo como marcador in silico de la enfermedad coronaria y producir una probabilidad de dicha enfermedad. El entrenamiento y la validación se realizaron en una cohorte de Estados Unidos y la prueba externa, en una cohorte del Reino Unido. El AUC fue el principal parámetro para el diagnóstico. Se presentaron sensibilidad, especificidad, exactitud, VPP y VPN, pero no se indicó el umbral utilizado para determinar estos parámetros. Esto es un ejemplo de la dificultad que comporta el lenguaje informático con el que los lectores clínicos no están familiarizados, ya que en el ámbito informático es un lugar común servirse de una probabilidad de 0,5 como umbral de clasificación. Sin embargo, en caso de que así hubiera sido en este artículo, debería haberse indicado. Tampoco se presentó un gráfico de calibración. Se hizo referencia a las puntuaciones de Brier, pero estas son inadecuadas y poco informativas por sí solas. En el artículo no se mencionó una curva de precisión-recuerdo y el gráfico de calibración mostrados en el apéndice. Este último mostraba que el algoritmo producía una sobrepredicción de la probabilidad de enfermedad coronaria para todos los casos excepto las predicciones más altas. Una característica muy positiva del estudio fue la demostración de una asociación de las probabilidades con la estenosis coronaria y la mortalidad por cualquier causa. No se realizaron comparaciones con otros modelos de predicción.
SÍNTESISAunque la era del AA ya ha llegado, todavía no se ha trasladado a la práctica clínica. Esto se debe en parte a que en los encargados de la toma de decisiones hay una curva de aprendizaje para comprender lo que es un estudio de AA bien realizado. En este artículo he intentado proporcionar cierta traducción entre el lenguaje de la informática y el lenguaje que resulta más familiar a un estadístico médico y he resaltado luego algunos parámetros de medición y medios gráficos que son útiles para evaluar los modelos de AA. Por último, he identificado algunos estudios que muestran diferentes elementos de AA en cardiología.
FINANCIACIÓNEl autor cuenta con el apoyo de donaciones realizadas al Christchurch Heart Institute y la Emergency Care Foundation, ambas de Christchurch, Nueva Zelanda.
CONFLICTO DE INTERESESEl autor no declara ningún conflicto de intereses.