Esta revisión es la segunda parte de 2 artículos sobre metodología estadística. En el primero, se describían los conceptos básicos del análisis de supervivencia y los métodos estadísticos más comúnmente utilizados y se aportaba un conjunto de recomendaciones para ayudar a establecer una estrategia de análisis de supervivencia, tanto en el contexto de un ensayo clínico aleatorizado como en el de un estudio observacional. En este segundo artículo, se introducen el modelo estratificado de Cox y el modelo de fragilidad y se ilustra el sesgo de tiempo inmortal secundario a una evaluación errónea de variables dependientes del tiempo. Para abordar el problema de la existencia de múltiples eventos clínicos, se introducen distintas aproximaciones estadísticas, como el análisis de riesgos competitivos, los modelos multiestado y el modelo de eventos recurrentes. Todos ellos se ilustran con ejemplos del campo cardiovascular, y se resumen las principales ventajas y limitaciones de cada uno de los métodos estadísticos. Por último, se presentan algunas consideraciones generales sobre métodos estadísticos alternativos, con asunciones menos restrictivas, como el método win ratio, el tiempo de supervivencia medio restringido y el modelo de tiempo de evento acelerado.
Palabras clave
Según los conceptos tratados en el artículo de revisión anterior1, este segundo artículo exploran situaciones más complejas en los análisis de supervivencia. A continuación se abordan algunas ampliaciones del modelo de riesgos proporcionales de Cox (RPC), tales como los modelos estratificados y de fragilidad, y el uso de las variables dependientes del tiempo. Se analizan los problemas que surgen en la investigación cardiovascular debido a la multiplicidad de eventos y se definen maneras de abordar esta cuestión: utilizar eventos compuestos, riesgos competitivos, modelos multiestado y métodos de eventos recurrentes. Un concepto cada vez más utilizado es el método win ratio (razón de ganancias sobre pérdidas). Para ofrecer una visión exhaustiva de los métodos estadísticos más frecuentes en los análisis de supervivencia, se introducen el tiempo de supervivencia medio restringido y el modelo de tiempo de evento acelerado. Para una mejor comprensión, se explica cómo se han aplicado estos métodos en estudios previos del ámbito cardiovascular. Esta revisión es principalmente descriptiva en cuanto a contenido y, por ello, no se requieren conocimientos matemáticos o estadísticos.
EXTENSIONES DEL MODELO DE RIESGOS PROPORCIONALES DE COXModelo de riesgos proporcionales de Cox estratificadoEl modelo de RPC es el más utilizado en el análisis de supervivencia. Cuando no proporciona un buen ajuste de los datos, pueden considerarse algunas extensiones. En el modelo de RPC estratificado, se asume que el modelo de RP se aplica dentro de grupos (o estratos) de individuos, en lugar de aplicarse al conjunto de la cohorte. Se incluyen en el modelo las variables del estudio que se dan por sentadas y satisfacen el supuesto de los RP, mientras que el factor por el que se estratifica no está incluido y se controla por la estratificación. Así pues, este método no proporciona una estimación del efecto del factor (o factores) que define los grupos en el riesgo (es decir, que no proporciona un cociente de riesgos instantáneos [hazard ratio] de las variables que se estratifican), por lo cual no es una estrategia apropiada si el factor que no cumple el supuesto de proporcionalidad es de máximo interés. Para evaluar qué efecto tenían los antagonistas del receptor de mineralocorticoides en la prevención de la muerte súbita cardiaca de los pacientes con insuficiencia cardiaca (IC) y fracción de eyección reducida, fue necesario un modelo de RPC estratificado que tratase las diferencias inevitables entre los 11.032 pacientes incluidos en los 3 ensayos clínicos aleatorizados (ECA) controlados con placebo: RALES (Randomized Aldactone Evaluation Study), EPHESUS (Eplerenone Post–Acute Myocardial Infarction Heart Failure Efficacy and Survival Study) y EMPHASIS-HF (NCT00232180). Aunque todos los pacientes tenían en común haber sufrido IC con fracción de eyección reducida, los que participaron en el estudio EMPHASIS-HF estaban en clase II de la New York Heart Association (NYHA), mientras que los del estudio RALES estaban en NYHA III-IV y los del estudio EPHESUS sufrieron un infarto de miocardio (IM)2. En otros casos, los modelos de RPC se estratifican por la región geográfica y la función renal basal3.
Modelos de fragilidadEn un modelo de RPC estratificado, las funciones de riesgo basales de los distintos estratos no se relacionan entre sí, asumiendo que la población en estudio sea homogénea en todos los estratos. No obstante, los sujetos pueden variar mucho dentro de los estratos (p. ej., en un ECA, en relación con el efecto del tratamiento, mientras que en un estudio observacional es en relación con el efecto de las covariables en una asociación determinada). La presencia de factores de riesgo específicos del individuo no recogidas da lugar a una heterogeneidad no observada en cuanto al riesgo, a la que también se hace referencia como fragilidad o efecto aleatorio. En muchas situaciones no puede suponerse que la población sea homogénea (p. ej., un conjunto de participantes con distintos riesgos). En este caso, al contrario que en el modelo de RPC, el modelo de fragilidad es útil porque implica que las funciones de riesgo iniciales son proporcionales entre sí.
Los modelos de fragilidad son modelos de efectos aleatorios para datos relativos al tiempo transcurrido hasta el evento4, en los que el efecto aleatorio tiene un efecto multiplicativo en la función de riesgo inicial. En el contexto de los modelos de supervivencia, este efecto aleatorio se denomina «fragilidad» por razones históricas, ya que el término simplemente se refiere al hecho de que algunos sujetos son intrínsecamente más «frágiles» que otros. Es el clásico ejemplo de un estudio en el que se incluye a pacientes de distintos hospitales. Los tiempos de supervivencia de los participantes del mismo hospital tienden a ser parecidos (por la forma de indicar un tratamiento, los recursos técnicos, etc.) y existe mayor variabilidad entre hospitales que dentro de un mismo centro. Los datos agrupados (o jerárquicos) requieren aplicar un modelo que tenga en cuenta los clústeres o conglomerados. Una forma de modelar la dependencia de los tiempos transcurridos hasta el evento agrupados es introduciendo un efecto aleatorio y específico del conglomerado: la fragilidad4. Este efecto aleatorio explica la dependencia, dado que, si se conociera la fragilidad, los eventos serían independientes. El empleo de modelos de fragilidad es relativamente frecuente; se han aplicado en algunos estudios que utilizan el registro EPICOR (Long-term Follow-up of Antithrombotic Management Patterns in Acute Coronary Syndrome Patients)5, donde además de ajustar por edad, sexo y otros factores de confusión pertinentes, el modelo estadístico tuvo en cuenta un efecto aleatorio (fragilidad compartida) en el nivel de hospital5.
Variables dependientes del tiempoA veces las variables explicativas cambian con el tiempo en un individuo (p. ej., tratamiento, presión arterial o tabaquismo). Estas variables se conocen como dependientes del tiempo, actualizadas en el tiempo o variables que varían con el tiempo. Si no se tiene en cuenta los cambios de estas variables que ocurren con el paso del tiempo, los resultados obtenidos del modelo de supervivencia pueden estar sesgados, y es lo que se conoce como sesgo de inmortalidad o sesgo de supervivencia6.
El tiempo inmortalidad se refiere al periodo de seguimiento durante el cual el evento de interés no puede ocurrir porque el sujeto aún no está expuesto6. Un sujeto no es literalmente inmortal durante este periodo, pero permanece libre de eventos hasta que se lo clasifica como expuesto. Al realizar el análisis, una consideración incorrecta de este periodo de tiempo sin exposición será origen del sesgo de inmortalidad6. Si el tiempo de seguimiento sin exposición de un sujeto se clasifica erróneamente como expuesto, los pacientes del grupo expuesto tendrán una ventaja inherente de supervivencia. Por consiguiente, el sesgo de inmortalidad deriva en falsos efectos protectores de la exposición. Se han hallado ejemplos clásicos del sesgo de inmortalidad en la literatura científica como, por ejemplo, en los estudios sobre trasplante cardiaco de Texas7 y Stanford8, y en ambos se concluyó que un trasplante cardiaco prolongaba la supervivencia de los pacientes que estaban en lista de espera para trasplante. No obstante, los datos se analizaron escasamente porque el trasplante cardiaco no se trató como una variable dependiente del tiempo. El tiempo de espera de todos los pacientes que estaban vivos hasta que recibieron un trasplante se clasificó como expuesto al trasplante (en lugar de no expuesto), y significó una ventaja en tiempo de supervivencia para el grupo de pacientes trasplantados. Las defunciones que tuvieron lugar mientras se esperaba un trasplante se adjudicaron a la cohorte de no trasplantados. Al no clasificar correctamente dichos periodos de seguimiento, el tiempo inmortal aumentó la tasa de mortalidad del grupo no trasplantado, lo que implicaba un beneficio «artificial» del trasplante9. No obstante, cuando más tarde se analizó correctamente, la mayor ventaja de supervivencia de la intervención desaparecía al clasificar de manera apropiada los tiempos de seguimiento10.
Cuando se estima el efecto de las covariables dependientes del tiempo, el periodo de seguimiento tiene que dividirse en subintervalos (tiempo hasta la exposición y tiempo desde la exposición en adelante), que significa que un sujeto podría tener más de un subintervalo (p. ej., más de una fila en el conjunto de datos, una para cada subintervalo). A los sujetos se los incluye vivos en el estudio, a la espera de la exposición, luego son censurados cuando se exponen, y comienza un nuevo subintervalo de tiempo (una nueva fila en el conjunto de datos) donde el tiempo de entrada es el tiempo censurado desde el primer subintervalo, con un nuevo valor de covariable que indica el periodo posexposición. En la cohorte del estudio EPICOR, Bueno et al.11 evaluaron cómo influían en la mortalidad la duración del tratamiento antiagregante plaquetario doble (TAPD) en los pacientes con síndrome coronario agudo y el cambio de TAPD a tratamiento antiagregante plaquetario en monoterapia (TAPM). El TAPD se introdujo en el modelo como una variable categórica actualizada (0 significaba estar en TAPD y 1, un cambio a TAPM). En el caso de los pacientes que siempre estuvieron en TAPD y por ello nunca en TAPM, el valor de las variables actualizadas fue 0 durante todo el seguimiento. De los pacientes que cambiaron de un TAPD a un TAPM (normalmente al cabo de 1 año de seguimiento), los autores proporcionaron los tiempos de seguimiento de ambos grupos (tiempo expuesto a TAPD y tiempo expuesto a TAPM).
Para estimar el impacto de las covariables dependientes del tiempo pueden utilizarse 2 métodos12: el modelo de RPC, que puede adaptarse a las variables dependientes del tiempo, y el análisis con punto temporal de referencia. Para este último método se debe establecer un momento de referencia y utilizar el valor de la covariable dependiente del tiempo en este punto de referencia como covariable fija en el tiempo. Con esta estrategia, se excluye del análisis de supervivencia a los participantes con un evento anterior al momento de referencia, dado que comenzará desde el punto temporal de referencia en adelante y en el subgrupo de participantes en riesgo en ese momento determinado.
MODELOS ALTERNATIVOS PARA LOS DATOS DE SUPERVIVENCIAEl modelo de RPC es el método más habitual para el análisis de datos del tiempo transcurrido hasta el evento. No obstante, este modelo de regresión no es apropiado en algunas situaciones, como cuando el hazard ratio no es constante en el tiempo13,14. Además, una limitación del modelo de RPC es que el hazard ratio es una medida relativa que no cuantifica efectos absolutos o asociaciones. Otros métodos pueden superar algunas de las limitaciones del análisis de RP. No obstante, cuando se satisfacen los RP, el modelo de RPC es el método con mayor potencia estadística13.
Tiempo de supervivencia media restringidoEl tiempo de supervivencia medio restringido (TSMR) es una medida de la supervivencia media desde el tiempo 0 a un momento determinado, y puede estimarse como el área bajo la curva de supervivencia hasta dicho punto13,14. Las asociaciones se expresan como la diferencia en el TSMR entre grupos en un momento apropiado del seguimiento, que es fácil de interpretar tanto por los médicos como por los pacientes (p. ej., si el evento de interés es la mortalidad, la estimación sería la pérdida de esperanza de vida). Además, la diferencia entre los TSMR proporciona una medida absoluta (p. ej., en un ECA con 2 ramas, el TSMR proporciona el beneficio o el daño absoluto). Este método no requiere ninguna suposición sobre los riesgos y tiene la ventaja de que es válido en cualquier distribución del tiempo de supervivencia o cuando se espera que una asociación varíe con el tiempo como, por ejemplo, una intervención con efectos inmediatos o tardíos.
El análisis del TSMR refleja toda la historia de supervivencia, no cambia cuando se extiende el tiempo de seguimiento y se relaciona sistemáticamente con un momento clínicamente significativo15. En los ECA de IC, parece que el TSMR añade valor a los análisis de RP tradicionales al proporcionar estimaciones clínicamente pertinentes de los efectos del tratamiento, junto con los resultados obtenidos por otros métodos estadísticos16.
Tiempo de fallo aceleradoEste método se conoce como modelo de tiempo de fallo acelerado porque el término «fallo» indica la muerte o evento, mientras que el término «acelerado» indica el factor por el cual la tasa de fallo se incrementa. Dicho factor se denomina «factor de aceleración»17. En lugar del riesgo, la medida clave de la asociación entre la variable del estudio y el tiempo de supervivencia es el factor de aceleración, que es un cociente de los tiempos de supervivencia. De un modo parecido al modelo de RPC, el modelo del tiempo de fallo acelerado explica la relación entre las probabilidades de supervivencia y un conjunto de covariables, y estima una asociación relativa (no absoluta). El modelo del tiempo de fallo acelerado proporciona una estimación del cociente de los tiempos medianos del evento, que para los médicos puede traducirse en la reducción esperada de la duración de la enfermedad con cierto tratamiento17.
MULTIPLICIDAD DE EVENTOS EN EL ANÁLISIS DE SUPERVIVENCIALos estudios clínicos pueden evaluar múltiples eventos para intentar maximizar la información proporcionada por dichos estudios. En el campo de la investigación cardiovascular, los eventos de interés podrían ser: ictus, IC, IM, muerte súbita, muerte cardiovascular o mortalidad por cualquier causa. Para evitar que se infle la probabilidad de error de tipo I al analizar cada evento por separado, una posible solución es utilizar un evento compuesto que incluya todos los eventos basados en el principio del tiempo transcurrido hasta el primer evento. Los eventos compuestos tienen varias ventajas18, pues engloban tanto eventos fatales como no fatales y así incrementan las tasas de eventos y la potencia estadística (por lo que se requieren muestras de menor tamaño o seguimientos más cortos)19.
Sin embargo, también tienen ciertas desventajas20, como el supuesto subyacente de que cada uno de los resultados individuales incluidos en un evento compuesto tiene una importancia similar para los pacientes21. También es frecuente que tanto la incidencia de eventos como el efecto del tratamientos sean mayores con eventos clínicamente menos relevantes22. Por ello, no siempre es óptimo utilizar eventos compuestos. En algunas situaciones se requieren estrategias estadísticas más sofisticadas que simplemente utilizar un evento compuesto basado en el tiempo transcurrido hasta el primer evento, tales como: a) analizar la presencia de riesgos competitivos en la evaluación de eventos no fatales, donde la aparición de eventos fatales puede sesgar los resultados; b) utilizar modelos multiestado que tengan en cuenta los estados intermedios (p. ej., antes de la muerte por causas relacionadas con IC, es frecuente el ingreso por IC)23; c) utilizar métodos de eventos recurrentes que registren globalmente la carga de enfermedades crónicas que implican varios ingresos durante el periodo de seguimiento, y d) utilizar el método de win ratio para obtener una evaluación jerárquica de cada uno de los componentes de un evento compuesto.
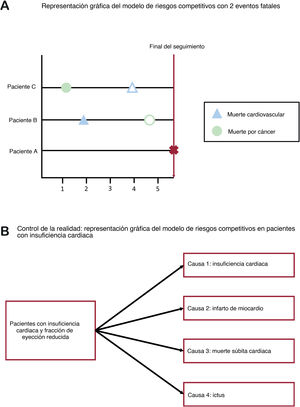
RIESGOS COMPETITIVOSEl supuesto de la censura estadísticaLa censura estadística no informativa o independiente es un supuesto aceptado para la mayoría de los métodos de análisis de supervivencia: los sujetos censurados corren el mismo riesgo de sufrir el evento de interés que los no censurados24,25. En otras palabras, los sujetos no censurados que permanecen en seguimiento deberían ser representativos de la experiencia de supervivencia de los sujetos censurados. No obstante, si se produce censura estadística por la aparición de otro evento conocido, se incumple la hipótesis de que la censura estadística no es informativa. Los riesgos competitivos tienen lugar cuando el evento de interés es una causa particular de «muerte» o fallo (p. ej., muerte cardiovascular), que puede tener lugar junto con otras causas de fallo (p. ej., muerte no cardiovascular debida a cáncer). El riesgo competitivo puede impedir que el evento de interés tenga lugar: una persona que muere de cáncer no correrá el riesgo de fallecer por una causa cardiovascular (figura 1).
Sesgo de los riesgos competitivos: impacto en la incidencia acumulada de eventosCuando la censura es informativa debido a múltiples causas de fallo, se introduce el sesgo de riesgos competitivos. Este sesgo se ha observado en casi la mitad de los análisis de Kaplan-Meier publicados en revistas médicas26. Si se estima la probabilidad de supervivencia en la muerte súbita de los pacientes con IC y fracción de eyección reducida y se censuran las otras causas de muerte (p. ej., muerte por IC), la incidencia acumulada de los eventos a lo largo del tiempo (que es 1 menos la probabilidad de supervivencia) sobrestimará la probabilidad de muerte debida a muerte súbita2. En efecto, al utilizar el estimador de Kaplan-Meier y censurar las otras causas de muerte, se presupone que los censurados por una muerte relacionada con IC corren el mismo riesgo futuro de muerte súbita que quienes aún no han sufrido ningún evento. Aunque esto no es cierto, ya que los que ya han fallecido por otros motivos no pueden fallecer de muerte súbita. Si se supone que los que ya han fallecido de otras causas siguen en riesgo de sufrir una muerte súbita y pueden estar representados por quienes aún no han sufrido ningún evento, el método de Kaplan-Meier sobrestima la probabilidad de fallo y subestima, por lo tanto, la probabilidad de sobrevivir en un momento determinado. Otro ejemplo clásico sería el de los pacientes con desfibrilador automático implantable27.
Estudio del análisis estadístico en los riesgos competitivosExisten 2 modelos de regresión distintos aplicables en situaciones en las que existen eventos competitivos28,29: la modelización del riesgo específico de la causa o la función de riesgos de la subdistribución.
- 1.
Función de riesgo de causa específica (uso de la función de incidencia acumulada [FIA]). La FIA estima la incidencia de un evento de interés al tiempo que permite la existencia de un riesgo competitivo. Los sujetos que padecen el evento competitivo dejan de considerarse en riesgo del evento de interés. En el caso más simple, cuando solo hay un evento de interés y no hay riesgos competitivos, la FIA sería igual a 1 – la estimación de Kaplan-Meier. La FIA tiene en cuenta ambas probabilidades de sufrir el evento de interés, condicionada a no experimentar ambos eventos (principal o competitivo) hasta ese momento. La suma de las estimaciones de la FIA para cada evento equivale individualmente a la estimación de la FIA del evento compuesto que consiste en todos los eventos competitivos. A diferencia de la función de supervivencia, en ausencia de riesgos competitivos, la FIA del evento de interés no necesariamente se acercará a la unidad con el tiempo, por la incidencia de eventos competitivos que impiden la aparición del evento de interés28. La FIA puede interpretarse como la tasa instantánea del evento principal en los sujetos que en el momento actual no sufren ningún evento.
- 2.
Modelo de Fine y Gray (uso de la función de riesgos de la subdistribución). Fine y Gray modificaron el modelo de RPC para permitir la presencia de riesgos competitivos30. La función de los riesgos de la subdistribución para un tipo determinado de evento se define como la tasa instantánea de aparición de dicho evento en los sujetos que aún no han sufrido ningún evento de ese tipo. Por ello, en este modelo, se considera la tasa del evento en los participantes que actualmente no han padecido el evento o que han sufrido con anterioridad un evento competitivo (aunque no parece natural mantener en el modelo a los participantes muertos en riesgo de otros eventos). Esto difiere del modelo establecido para la función de riesgo de causa específica, que solo incluye a quienes actualmente no han sufrido ningún evento. De este modo, hay una función de riesgos de la subdistribución para cada evento (p. ej., uno para la muerte súbita y otro para la muerte relacionada con la IC).
El modelo de la FIA estima el impacto de las covariables en la función de riesgos específicos de la causa, mientras que el modelo de riesgos de la subdistribución de Fine-Gray estima el impacto de las covariables en la función de riesgos de subdistribución27. Puesto que el modelo de la FIA se basa en los participantes en riesgo (participantes que no sufren ningún evento), el cociente de riesgos de este modelo debería interpretarse entre los sujetos que todavía no han experimentado el evento de interés o el evento competitivo y, por lo tanto, este método es óptimo para responder a las preguntas de investigación etiológica. Al contrario, al mantener en el modelo a los sujetos que han experimentado el evento competitivo, el modelo de riesgos de la subdistribución puede ser de gran interés para el estudio del impacto global de las covariables en la incidencia del evento de interés y es óptimo para realizar escalas predictivas y puntuaciones de riesgo31.
MODELOS MULTIESTADODefinición de eventos absorbentes y no absorbentesUn evento absorbente impide que el evento de interés tenga lugar con posterioridad (p. ej., una muerte cardiovascular impide una muerte por cáncer). A veces hay un evento intermedio, que tiene lugar antes del evento absorbente y se conoce como evento no absorbente. Estos eventos intermedios tienen especial interés cuando su aparición cambia de manera sustancial la probabilidad de que el evento de interés tenga lugar y, por lo tanto, proporcionan información más detallada de la evolución natural de la enfermedad. El evento intermedio puede interpretarse como un deterioro o una mejora de la evolución de la enfermedad. Este paso fue ilustrado por Solomon et al.23, quienes evaluaron cómo influían las hospitalizaciones no fatales por IC en la mortalidad posterior de los pacientes con IC crónica. En contraposición al riesgo de mortalidad relativamente estable observado a lo largo del tiempo en pacientes con IC del ensayo clínico CHARM (Candesartan in Heart failure: Assessment of Reduction in Mortality and morbidity), estos autores observaron una mayor probabilidad de fallecer en el periodo inmediatamente posterior al alta tras la hospitalización por IC que se relacionó directamente con la duración y la frecuencia de la hospitalización por IC23. Así, haber sido hospitalizado por un episodio de IC (evento no absorbente) cambió el riesgo del evento de interés (mortalidad).
Los eventos no absorbentes pueden analizarse con modelos multiestado32, en los que el foco de atención se sitúa en el cambio de estado a lo largo del tiempo (p. ej., cambios desde el estado inicial hasta la hospitalización por IC y desde este momento hasta la muerte cardiovascular)33.
Modelos multiestado: una ampliación de los modelos de riesgos competitivosLos modelos multiestado proporcionan un marco para el análisis de la evolución natural de una enfermedad. Estos modelos son una ampliación de los modelos de riesgos competitivos (modelo multiestado con un estado inicial y varios estados absorbentes mutuamente excluyentes), dado que extienden el análisis a lo que ocurre tras el evento intermedio34. En esta revisión solo se tendrán en cuenta los modelos de tiempo continuo que permiten cambios de estado en cualquier momento. Estos modelos son más realistas y se consideran una ampliación del modelo de supervivencia estándar, porque explican cómo un sujeto pasa por una serie de estados aislados en el tiempo continuo.
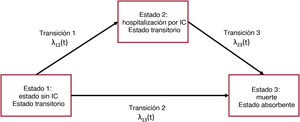
Los modelos multiestado son apropiados cuando la enfermedad conlleva transiciones entre diversos estados bien diferenciados. Un modelo de supervivencia de 2 estados se define por un estado vivo y un estado muerto. Las 2 principales características del modelo de supervivencia estándar son: a) hay un evento de interés (la transición de estar vivo a estar muerto), que es unidireccional, y b) la sincronización de este evento puede estar censurada por la derecha, en cuyo caso se sabe que el evento aún no ha ocurrido. Una curva de Kaplan-Meier puede considerarse un modelo multiestado simple con 2 estados y una transición entre dichos 2 estados. La situación se complica cuando se incluyen en el modelo eventos no absorbentes. En el contexto de la IC, la hospitalización por IC puede definirse como un evento transitorio (evento no absorbente). En un modelo de supervivencia de 3 estados, se diferenciarían: un estado sin IC, un estado con IC y un estado de muerte. Esto establece 3 eventos: muerte en el estado 1 (estado sin IC), muerte en el estado 2 (estado con IC) y transición del estado sin IC a la hospitalización por IC (figura 2). Las tasas de riesgo del paso de un estado a otro se definen como intensidades de transición, el riesgo instantáneo de pasar de un estado a otro en un momento determinado. Estas intensidades de transición son equivalentes a los riesgos específicos descritos en el método de riesgos competitivos, situación que es un caso particular de los modelos multiestado. Hay tantos riesgos por modelar como transiciones.
Para ejecutar un modelo multiestado, se utiliza una estructura de datos de proceso de recuento. Así pues, cada vez que hay una transición, se requiere una nueva fila de información para el conjunto de datos de dicho individuo. En cambio, en un análisis de supervivencia tradicional del tiempo transcurrido hasta el primer evento, en el conjunto de datos solo hay una fila de información por paciente, que incluye el estado y el tiempo de supervivencia (tiempo transcurrido hasta el evento o tiempo hasta ser censurado).
Las recurrencias de una IC no fatal o un IM son eventos no absorbentes que dependen del tiempo. Aunque en los modelos de supervivencia estándar pueden tenerse en cuenta incluyendo el evento no absorbente como si fuera una covariable dependiente del tiempo para el riesgo de muerte, el mejor método para abordar estas transiciones de los pacientes por varios estados es mediante la modelización multiestado35. Para comprender mejor el pronóstico, un modelo exhaustivo debería incluir tanto la muerte como los eventos clínicos no fatales. Los modelos de RPC no son apropiados, puesto que las observaciones no son independientes. Los modelos multiestado superan esta limitación porque evalúan por separado el tiempo transcurrido hasta la muerte y las hospitalizaciones relacionadas con el tiempo transcurrido hasta la enfermedad36.
Modelos multiestado en cardiologíaEn varios estudios se han utilizado modelos multiestado en el campo de la investigación cardiovascular37. Además del clásico ejemplo de la IC crónica36, pueden hallarse otros ejemplos en pacientes con enfermedad coronaria multivaso. Con base en los datos del ensayo BARI (NCT00000462), Zhang et al.38 llevaron a cabo un modelo multiestado, donde el estado inicial correspondía a los pacientes tras la aleatorización y antes de la intervención; el estado intermedio, al IM no fatal y el estado final, a la muerte. En los análisis de supervivencia estándar con regresión de Cox y estimación de Kaplan-Meier, tanto para la mortalidad como para el evento compuesto por muerte o IM no fatal, no se observaron diferencias entre la cirugía de revascularización y la angioplastia coronaria percutánea tras un seguimiento de 10 años. Cabe destacar que con este enfoque no se tuvo en cuenta el estado intermedio (IM no fatal). En cambio, con el modelo multiestado se separó el proceso en 3 transiciones y se observaron diferencias considerables que favorecían la cirugía de revascularización coronaria en pacientes en transición de un IM no fatal a la muerte, mientras que en los pacientes que no habían tenido un IM no hubo diferencias en la supervivencia entre los que se sometieron a cirugía de revascularización coronaria y los tratados con angioplastia coronaria percutánea. Este estudio muestra que con los eventos compuestos no se obtiene una información pronóstica tan precisa como con un modelo multiestado.
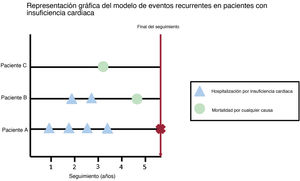
MÉTODOS DE EVENTOS RECURRENTESDefinición de evento recurrenteLa mayor parte de los estudios evalúan objetivos sobre el tiempo transcurrido hasta el primer evento, de modo que todos los eventos posteriores se ignoran en el análisis. En el ámbito de la IC, este problema pasa a ser aún más importante, dado que el análisis del «tiempo transcurrido hasta el primer evento» no refleja por completo la carga real de la enfermedad39: De los pacientes ingresados en servicios de urgencias hospitalarios españoles por IC aguda, el 24% reacudió dentro de los 30 días y el 16% fue rehospitalizado durante el mismo periodo de seguimiento40. Cabe destacar que cada siguiente hospitalización por IC implica un empeoramiento considerable del pronóstico a largo plazo41. A diferencia de los métodos convencionales, los métodos de eventos recurrentes tienen en cuenta la carga de enfermedad (figura 3).
Representación gráfica del modelo de riesgos recurrentes. Ilustración de varias situaciones en el contexto de eventos recurrentes: el paciente A ingresa 4 veces durante el seguimiento (solo el primer evento serviría en los análisis de supervivencia convencionales), el paciente B ingresa 2 veces antes de morir (aplicando los métodos tradicionales, solo se tendría en cuenta el primer ingreso) y el paciente C muere durante el seguimiento sin ningún ingreso previo (con un evento compuesto, la información sobre la carga de la enfermedad se perdería).
En general se supone que los métodos de eventos recurrentes mejoran la precisión y proporcionan mayor potencia estadística que los métodos convencionales del tiempo transcurrido hasta el primer evento. Por ejemplo, en el ensayo CHARM-Preserved42 se obtuvo un resultado no significativo en el análisis del tiempo transcurrido hasta el primer evento compuesto. No obstante, los análisis a posteriori con el método de eventos recurrentes demostraron un aumento significativo de la potencia estadística que desvelaba la eficacia del tratamiento19.
Análisis estadístico en los métodos de eventos recurrentesSon varios los métodos estadísticos que tratan la cuestión de los eventos recurrentes, pero hay cierta controversia en cuanto a cuál de ellos es el más apropiado. Existen 2 enfoques principales: a través de los recuentos (o tasas de eventos) y a través de los tiempos entre los eventos posteriores. En ambos casos se asumen tiempos censurados no informativos.
El primer enfoque se basa en la medición del número de eventos (es decir, el número de ingresos debidos a empeoramiento de la IC), y tiene 2 métodos fundamentales43. La distribución de Poisson es el modelo de recuento más conocido y puede utilizarse para determinar si la incidencia del evento difiere entre grupos, mientras que la distribución binomial negativa es un enfoque alternativo que permite que existan distintas tendencias individuales (fragilidades). Este último enfoque se ha utilizado de manera retrospectiva para evaluar las hospitalizaciones recurrentes en el ensayo EMPHASIS-HF44. En el ensayo TOPCAT (NCT00094302), el modelo de regresión de Poisson preestablecido se sustituyó por un modelo binomial negativo que consideró los eventos interdependientes45.
Hay muchos métodos para el segundo enfoque, que se basan en el principio del tiempo transcurrido hasta el evento. El enfoque de Andersen-Gill es una ampliación del modelo de RPC, que analiza los eventos recurrentes como tiempos entre intervalos (p. ej., los momentos entre eventos consecutivos)46. El método de Lin-Wei-Yang-Ying es un modelo de Anderson-Gill modificado, con un estimador robusto de la varianza que explica la correlación o interdependencia entre eventos, que es útil cuando las covariables se consideran dependientes del tiempo. Este enfoque se utilizó para el evento principal de todos los ingresos por IC (primera y recurrente) y las muertes cardiovasculares en el ensayo PARAGON-HF47. El método de Ghosh y Lin ofrece una estimación no paramétrica del número acumulado de eventos recurrentes a lo largo del tiempo, que incorpora la muerte como un riesgo competitivo48.
Comentarios finales sobre los métodos de eventos recurrentesParece que los modelos de eventos recurrentes proporcionan mayor potencia estadística que los enfoques basados en el tiempo transcurrido hasta el primer evento49. No obstante, la relativa amplitud de los intervalos de confianza del 95% relacionados con los análisis de eventos recurrentes a veces son mayores que en los análisis del tiempo transcurrido hasta el primer evento, lo que indica una pérdida de precisión19. Con datos de distintos ensayos (CHARM, TOPCAT, PARADIGM-HF [NCT01035255]), Clagget et al. observaron que la creciente heterogeneidad del riesgo de los pacientes, considerado un parámetro no incluido en las fórmulas convencionales de potencia y tamaño de la muestra, podría explicar las diferencias entre los análisis del tiempo transcurrido hasta el primer evento y de eventos recurrentes en lo que respecta a la estimación del efecto del tratamiento, la precisión y la potencia estadística49. En dicho estudio, se concluyó que las mayores ventajas estadísticas al utilizar métodos de eventos recurrentes tienen lugar en presencia de mucha heterogeneidad entre los sujetos y con una incidencia baja de interrupción del fármaco del estudio49.
MÉTODO WIN RATIO (RAZÓN DE GANANCIAS SOBRE PÉRDIDAS)Pocock et al.50 introdujeron en el año 2012 el método win ratio como un nuevo método para investigar los eventos compuestos, y se ha hecho cada vez más popular en los ECA cardiovasculares51,52. A diferencia de los métodos tradicionales que evalúan eventos compuestos, el método de win ratio tiene en cuenta las prioridades relativas de sus componentes e incluso permite distintos tipos de componentes. Por ejemplo, el win ratio puede combinar el tiempo hasta la muerte con el número de apariciones de un evento no fatal como, por ejemplo, las hospitalizaciones por causas cardiovasculares (HCV) en un único evento compuesto jerárquico. También puede incluir eventos cuantitativos, tales como las puntuaciones sobre la calidad de vida.
Según el principio de la prueba de Finkelstein-Schoenfeld, el método win ratio proporciona una estimación del efecto del tratamiento (el win ratio) y el intervalo de confianza, además de un valor de p53. En un ECA simple con 2 grupos, la aplicación del método win ratio puede resumirse en lo siguiente: a) se establecen todos los pares de sujetos posibles (cada paciente del grupo que recibe tratamiento se compara con cada paciente del grupo de control), y b) de cada par, se evalúan eventos de cada uno de ellos en orden descendente en importancia hasta que un par muestra un mejor resultado que el otro. Si el paciente del grupo que recibe tratamiento obtiene el mejor resultado, se habla de una «ganancia»; si la obtiene el paciente del grupo de control, se habla de «pérdida», y si no se produce ninguna de estas situaciones, se trata de un «empate».
Este enfoque se utilizó en el ATTR-ACT52, un ensayo a doble ciego en el que se aleatorizó a 441 pacientes con miocardiopatía amiloidea causada por depósito de transtirretina a tafamidis (80 y 20mg) o el placebo correspondiente durante 30 meses. En el análisis principal, los investigadores evaluaron de forma jerárquica la mortalidad por cualquier causa, seguida de la frecuencia de las HCV con los métodos de Finkelstein-Schoenfeld53 y win ratio50. Para cada par, se determinó si el paciente que recibía tafamidis «ganaba» o «perdía» comparado con el paciente que recibía placebo. La evaluación jerárquica consistió en determinar: a) quién fallecía primero (el «perdedor»), y luego b) si nadie fallecía, quién sufrió más HCV (de nuevo el «perdedor»), y se evaluó a ambos durante el periodo de seguimiento compartido. Tras la suma, se obtuvo un total de 8.595 ganadores y 5.071 perdedores. Así pues, el win ratio fue de 8.595/5.071=1,70, con un intervalo de confianza del 95% de 1,26-2,29 y p=0,000654. Con los métodos tradicionales, en la evaluación de un evento compuesto de la primera HCV o muerte se habrían omitido las HCV repetidas que tuvieron lugar después de la primera HCV, así como cualquier defunción que ocurriera después de una HCV. El win ratio proporciona mayor potencia estadística para estimar las diferencias en el tratamiento al evaluar de manera jerárquica cada uno de los componentes de un evento compuesto.
OTROS ENFOQUES: MODELIZACIÓN DE REGRESIÓN LOGÍSTICA Y DE POISSONAdemás de los modelos de RPC, los datos de supervivencia a menudo se evalúan con el modelo de regresión logística y de Poisson55,56. La elección del tipo de modelo se basa en el diseño del estudio y el tipo de pregunta de la investigación57. En la tabla 1 se resumen las principales diferencias entre estos modelos en el contexto del análisis de supervivencia.
Resumen de las diferencias entre el modelo de riesgos proporcionales de Cox, el de Poisson y la regresión logística
| Modelo de riesgos proporcionales de Cox | Modelo de regresión de Poisson con intervalos | Modelos de regresión logística | |
|---|---|---|---|
| Pregunta de la investigación | ¿Cuánto tiempo pasa antes de que ocurra el evento en un periodo de tiempo determinado? | ¿Cuántas veces ocurre el evento durante un periodo de tiempo determinado? | ¿El sujeto sufre el evento en un marco de tiempo determinado? |
| Modelización | Modela los tiempos de supervivencia | Modela la incidencia del evento independientemente del tiempo | Modela si un evento ocurre o no |
| Uso del tiempo de supervivencia | Análisis de los tiempos de supervivencia individuales | Análisis agregado de la tasa de mortalidad de los pacientes | Análisis de tan solo los eventos, sin tener en cuenta cuándo tienen lugar. No utiliza los tiempos de supervivencia |
| Tipo de evento | Tiempo transcurrido hasta el evento | Datos de recuento del evento | Evento dicotómico |
| Tipo de asociación | Hazard ratio | Cociente de la tasa de incidencia | Odds ratio |
| Principal supuesto | La función de riesgo o la tasa de mortalidad son proporcionales entre los grupos | La tasa de eventos o el cociente de riesgos relativos permanecen constantes en intervalos de tiempo específicos o son proporcionales entre sí | No requiere que las variables dependientes y las independientes se relacionen de manera lineal, sino que las variables independientes estén en relación lineal con los cocientes logarítmicos |
Esta segunda revisión se centra en los modelos de RPC estratificados, los modelos de fragilidad y las variables dependientes del tiempo. Se han introducido los riesgos competitivos, los modelos multiestado, los métodos de eventos recurrentes y el método win ratio para abordar la cuestión de la multiplicidad de eventos, cuando los eventos compuestos y el tiempo transcurrido hasta el primer evento no sean lo óptimo. También se han explicado los métodos de los modelos de tiempo de supervivencia medio restringido y de tiempo acelerado. El tratamiento adecuado de los datos de supervivencia no suele ser sencillo y esta revisión ofrece consejos prácticos sobre lo que debería tenerse en cuenta antes de elegir el modelo más apropiado para el análisis de los datos de supervivencia, así como una guía para interpretar los resultados obtenidos con métodos estadísticos más complejos.
FINANCIACIÓNNinguna.
CONTRIBUCIÓN DE LOS AUTORESX. Rossello y M. González-Del-Hoyo concibieron la revisión. X. Rossello dirigió el proceso de redactado y M. González-Del-Hoyo se encargó de buscar la mayoría de los ejemplos para ilustrar los métodos. X. Rossello redactó el artículo, aunque ambos autores contribuyeron de manera sustancial en su revisión.
CONFLICTO DE INTERESESNinguno.