INTRODUCTION

One of the most important challenges when assessing the effect of a therapeutic intervention is the choice of the primary outcome measure.1 This variable, which represents the hypothesis that prompted the trial, should be clinically significant (important for the patient), readily assessed, free of bias, cheap to measure, and sensitive to the study intervention.2 It is hard to find a single measure that meets all these requirements. In addition, assessment of the effect of interventions is complex, as a single intervention usually acts on several aspects of a pathophysiological process or, if it does act on a single aspect, it nevertheless usually affects several organs and body systems. Side effects, whether predictable or unknown, may also arise. For these reasons, the investigators will often formulate more than 1 primary hypothesis. For example, an investigator could pose the following questions: Is intervention A effective at reducing the mortality in the study population?; Is intervention A effective at reducing the proportion of nonfatal myocardial infarctions?; Is intervention A effective at reducing the number of nonfatal strokes?

The logical approach to find answers to these 3 questions would be to conduct a randomized clinical trial (RCT) with 3 primary outcome measures: death, nonfatal acute myocardial infarction (AMI), and nonfatal stroke. Once finished, the results of the intervention on the 3 measures would be presented. However, in the current medical literature an increasing number of clinical trials are being published in which the various outcome measures are combined into a single outcome measure, which is known as the composite endpoint (CEP) or, alternatively, the combined endpoint or composite outcome. These CEPs combine in a single endpoint the number of patients who present with at least 1 of the individual components.3 In the previous example, the corresponding CEP would be death or nonfatal myocardial infarction or stroke. This approach pools the 3 previous questions into 1: Is intervention A effective at reducing the outcomes of death or nonfatal infarction or stroke? The 2 approaches clearly differ in nature as, when CEPs are used, the subsequent analysis does not correspond to the primary hypothesis of the study.

In the discussion below, with reference to a systematic review of the use of the main CEPs,4 we make a critical analysis of the rationale for their use, as well as the limitations and pitfalls. We also present guidelines for their interpretation.5 Finally, we present empirical evidence of the problematic use of CEPs in cardiovascular RCTs.6

RATIONALE BEHIND THE USE OF COMPOSITE ENDPOINTS

A recent systematic review of the rationale and pitfalls of RCTs found 17 articles on the topic.4 This review showed that theoretical knowledge of the problems of CEPs has yet to be satisfactorily addressed and that methodologies disagree about many aspects of the use of these measures. Furthermore, the review identified the following 3 basic situations in which CEPs were often used.

Decrease in Sample Size Required to Show Effects

In line with the previous example, suppose that an investigator decides to conduct an RCT to assess the 3 primary hypotheses. In order to answer each of these, this strategy requires a sample size calculation that includes the following variables: the expected proportion of events, type I (a) and type II (b) errors, and the size of the effect expected from the intervention. Suppose that the investigator wanted to show a relative risk reduction (RRR) of 20% for each of the primary endpoints, with a statistical power of 80% (type II error of 20%) and a type I error of 5%. Suppose also that the sample size calculation yields the following figures: in the case of AMI, 1000 patients would be required; in the case of stroke, 5000 patients would be required; in the case of mortality, 20 000 patients would be required. If the investigator wanted to test the 3 previous hypotheses with sufficient statistical power, he or she should include at least 20 000 patients.

Now suppose that the investigator decides to conduct an RCT using the CEP "death or nonfatal AMI or stroke." The expected effect of the intervention is, as in the previous case, 20% and the type I and type II errors are also the same. However, the fourth parameter, the expected proportion of events is clearly different: the proportion of patients who, during follow-up, will suffer at least 1 of these events is substantially greater, thereby leading to a decrease in sample size, which will be larger the smaller the level of dependence or correlation between the components.1 Thus, in the "best" case scenario (that is, that no pairwise correlations among the 3 were present), a RRR of 20% in the CEP could be demonstrated with only 1000 patients.

It is currently increasingly difficult to demonstrate the effect of an intervention as most patients are medicated and their prognosis is considerably better than a few decades ago. This in turn requires increasingly large trials to be conducted (megatrials), with longer follow-up, to reach a sufficient number of events (deaths, infarction, etc). Such trials are, however, more difficult to conduct in terms of logistics and cost. A way to overcome this problem is to use CEPs.

Now, if intervention A reduces the RRR of "death or nonfatal AMI or stroke" by 20%, what does this mean? What can be inferred about the effect of the intervention on each of the individual components?

Assessment of the "Net" Effect of an Intervention

Suppose that the invention in question is associated with a clinically significant risk. For example, a new thrombolytic agent is under investigation for treatment of AMI. Thrombolytic therapy increases the risk of cerebral hemorrhage and the investigator believes that the new thrombolytic agent—much more effective than standard thrombolytic therapy—is associated with lower risk. It is decided to conduct an RCT with both types of thrombolytic agent with the CEP of "death or cerebral hemorrhage."

In this scenario, the CEP is not used for decreasing the required sample size given that it is expected that the direction of the effect of the intervention on the outcome of death works in the opposite direction to the effect of the outcome of cerebral hemorrhage (that is, it is expected that thrombolytic therapy is effective at reducing the number of deaths but that it increases the number of cerebral hemorrhages compared to standard therapy). The use of this CEP will be less efficient at showing an effect than would be, for example, an individual outcome such as "death," which is expected to yield a greater net decrease in the number of events. What then is the rationale behind using this CEP? The answer is simply to capture the "net benefit of the intervention." In the previous example, it would be of little use if the new thrombolytic agent reduced mortality somewhat but greatly increased the number of cerebral hemorrhages. A simple strategy for assessing the effect of interventions associated with important clinical risks is using a CEP that combines "efficacy" and "safety" outcomes. If the new intervention leads to a statistically significant decrease in the percentage of the events making up the CEP, we can be certain that this intervention is, in general, more beneficial than the standard one.

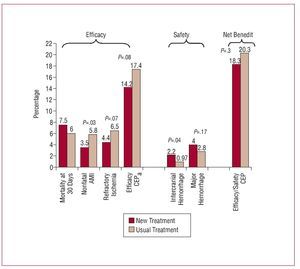
A similar example is shown in Figure 1. A recent clinical trial assessed the efficacy and safety of tenecteplase in combination with low molecular weight heparin versus the same thrombolytic agent associated with unfractionated heparin.7 Although the new combination was more beneficial than the traditional one in terms of the "efficacy" outcome, the same could not be said of the "safety" outcome, which showed the new treatment to be harmful. The overall CEP, which expresses the overall net benefit of the new treatment, was therefore able to demonstrate a clear decrease in overall benefit.

Figure 1. Findings of a clinical trial to assess the efficacy of a new therapeutic regimen associated with tenecteplase. AMI indicates acute myocardial infarction, CEP, composite endpoint.

Now suppose that the investigator has reason to believe that the new thrombolytic therapy is effective at reducing the size of AMI and decides to use the CEP "death or cerebral hemorrhage, or presence of new pathology Q waves in the electrocardiogram." The results reflect substantial benefit associated with new treatment due to a reduction in the number of patients with "new pathologic Q waves," but with an increase in the number of cerebral hemorrhages and little effect on mortality. Can we be sure in this case that the CEP can capture the net benefit of the intervention? Should the new thrombolytic agent be classed as generally more beneficial than standard treatment in the event that a statistically significant reduction in the CEP is observed? In this case, it may be problematic to "trust" the overall result of the intervention, as there is a marked gradient in the importance of the components of the CEP. The outcome "presence of new pathologic Q waves," of less clinical significance, has a similar influence on the final result as the other 2 outcomes (death and cerebral hemorrhage) and manages to shift the net effect to a biased potential benefit.

Assessment of the Effect in Presence of Competing Risks

Sometimes, the underlying reason for using CEPs is not to reduce the required sample size or the need to capture the net benefit of an intervention, but rather to avoid bias in the assessment of an effect in the presence of competing risks.

The possibility of bias due to competing risks arises in situations in which the occurrence of an event decreases the probability of another event of interest occurring. For example, suppose that the investigator has reason to believe that an intervention decreases the risk of nonfatal AMI. The patients who die before suffering the event of interest have a nonexistent risk of suffering nonfatal AMI. In this case, the "competing event" is death. Imagine that a treatment does not have any effect on risk of AMI but that during the clinical trial, more deaths occur in the new treatment group than in the control group by chance or because of side effects associated with the new treatment. The overall "risk" of AMI in the treatment group is less as there are fewer patient-years of follow-up in the treatment group. In this case, if we were to compare the rate of AMI in both groups, it may be that the treatment appears more effective than it actually is at reducing the number of myocardial infarctions. Now, if instead of using the individual outcome measure of "nonfatal AMI," the CEP of "death or nonfatal AMI" is used, the possible bias due to competing risks is abolished as both outcomes are equivalent for the purposes of the analysis.

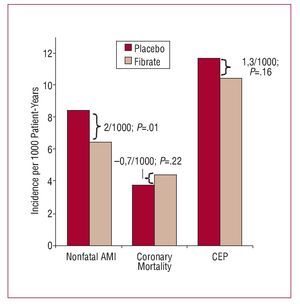
A similar situation can be seen in a recent RCT that analyzed the efficacy of fibrates in primary cardiovascular prevention in diabetic patients.8 In that study, nonfatal AMI was one of the outcomes of interest. The incidence of nonfatal infarction in the treatment group was significantly lower than in the placebo group: 6.4/1000 patient-years at risk versus 8.4/1000 patient-years at risk (P=.01). However, the incidence of death due to coronary disease was somewhat higher in the treatment group: 4.4/1000 patient-years versus 3.7/1000 patient-years (P=.22) (Figure 2). The analysis of the CEP "death due to coronary disease or nonfatal AMI" did not show a statistically significant benefit: 10.4/1000 in the treatment group versus 11.7/1000 in the control group (P=.16). We therefore cannot rule out the possibility that the treatment effect observed with the measure "nonfatal AMI" is partly an artifact introduced because of the presence of competing risks factors. In this specific example, the lack of effect observed in the CEP shows how this might be useful for avoiding a possible spurious effect in one of the components of the endpoint due to bias caused by competing risks factors.

Figure 2. Findings of a randomized clinical trial of fibrates versus placebo in primary cardiovascular prevention. AMI indicates acute myocardial infarction, CEP, composite endpoint.

Finally, we should mention that the analysis of competing risk factors is not just confined to RCTs. In fact, this analysis strategy has been applied to cohort studies, for example in the field of AIDS.9

INTERPRETATION OF THE FINDINGS OF CLINICAL TRIALS BASED ON COMPOSITE ENDPOINTS

As discussed previously, the use of CEPs doubtlessly has some advantages. However, if they are not analyzed in terms of the rationale behind their use, the interpretation of the effect of an intervention may be erroneous. The CEPs are, therefore, a double-edged sword that should be treated extremely carefully and with full awareness of the ambiguities which some studies fail to clarify. Unfortunately, in the medical literature, it is often difficult to determine the rationale behind the use of CEPs in RCTs, particularly when the sponsor of a trial with a particular drug may prefer to focus on a positive result based on a CEP rather than to enter into debate about the precaution needed in the interpretation of the treatment effect.

It is therefore up to the reader to evaluate the risk of spurious interpretation of the outcome of an intervention measured with a CEP. The biggest risk occurs when a clearly positive effect is found for the CEP but when this effect is due mainly to a component of little clinical significance, whereas the effect for clinically significant components is null or even negative.

Montori et al5 have recently proposed guidelines for interpretation that aim to assess the risk of inaccurate interpretation of results based on CEPs. Although the reasons for using CEPs are not contemplated in these guidelines—a potential limitation to their use in some cases—they represent the first useful step forward for differentiating between clinical trials with a simple interpretation of results based on CEPs and those in which such an interpretation is more complex. The guidelines pose 3 basic questions: Would the patients consider the components of the CEPs to be of similar importance? Were the frequencies of the different components similar? Were the effects of the intervention similar for each of the components? Our confidence in the assessment of the effect based on CEPs will be progressively eroded when we encounter larger differences in importance to the patients, frequency, and treatment effects.

We now present 2 illustrative examples of CEPs in which the risk of spurious interpretation is minimized (first example) and maximized (second example).

Example 1: HOPE Study10

In this study, 9297 patients with cardiovascular risk factors were randomized to receive ramipril or placebo. The CEP of "AMI or cerebrovascular accident or cardiovascular death" was used. Table 1 shows the results of the intervention on the CEP and on each of its components.

Example 2: DREAM Study11

In the DREAM study, 5269 patients with no documented cardiovascular disease and glucose intolerance were randomized to rosiglitazone or placebo. The CEP "incident diabetes or death" was used. The results are presented in Table 2.

Importance of the Components (Would the Patients Consider the Components of the CEPs to Be of Similar Importance?)

The components included in a CEP should be of similar importance for the patients. If this were not the case, erroneous conclusions could be reached through mixing very different results. If we analyze the heterogeneity of the CEP in terms of the importance of their components in previous examples, the difference is readily apparent. Whereas in the HOPE study there is a certain gradient in the importance of the components (AMI or cerebrovascular accident, or cardiovascular death), this is much smaller than the one in the second example, where both components are very different in terms of importance to the patient (incident diabetes or death). Although this analysis is clearly subjective, it can serve as a first step towards classifying the most problematic cases which, it must be said, are not unheard of in the literature.

Frequency of Events (Did the Components Occur With Similar Frequency?)

The larger the variation in frequency of events of the different components in the control group, the greater the uncertainty about the applicability to these components of the effect of the intervention measured by CEP. While in the components with a high frequency of events, the precision of the estimator of effect will also be high, in those with low frequency of events, the uncertainty about that estimator will be much greater, and this will complicate the interpretation of the effect. This strategy serves as a guide to distinguishing which situations are more problematic than others. The previous examples provide an illustrative example. While the distribution of events in the control group in the HOPE study varied between 4.9% and 12.3%, in the DREAM study, the heterogeneity of the frequency of events was markedly higher: 1.3% for death and 25% for the outcome "incident diabetes."

Homogeneity of the Effect (Was the Effect of the Intervention Similar for Each of the Components?)

It is important to examine the effect on the different components to look for the degree of variability among them. The degree of variability, if marked, indicates that the effects on the components of a CEP may vary greatly thereby bringing into question their combined evaluation. As in the previous case, the estimator of the effect of the intervention on the components (expressed in the form of relative risk or hazard ratio) is relatively homogeneous in the HOPE study, ranging from 0.7 to 0.8, and very heterogeneous in the DREAM study, ranging from 0.38 to 0.9. Whereas in the first study we can affirm that the effect of the intervention on the CEP can be applied to the rest of its components, in the second study, this is not the case.

Combining the 3 previous questions, we can conclude that, whereas it is expected that the effect of the intervention on the CEP can be applied to its components in the HOPE study, in the DREAM study there is very strong uncertainty as to whether this applies. Furthermore, the most prudent inference that we can make with the DREAM study is that it is plausible that the intervention has a beneficial effect on the risk of incident diabetes. In contrast, we cannot draw any conclusions about the "overall mortality" component.

Nevertheless, the authors of the DREAM study concluded that this large international, prospective, blinded clinical trial showed that rosiglitazone at 8 mg daily, along with diet and lifestyle recommendations, substantially reduces the risk of diabetes or death in 60% of the individuals at high risk of diabetes. While this statement is correct, clearly the affirmation that the intervention reduces the risk of diabetes or death by 60% gives the reader the impression that the intervention is beneficial for both components, a fallacious conclusion that exaggerates the treatment effect observed in the trial.

USE OF POTENTIALLY PROBLEMATIC COMPOSITE ENDPOINTS IN CARDIOVASCULAR CLINICAL TRIALS

In order to explore the use of potentially problematic CEPs actually used in the cardiovascular field, a study was conducted of the RCTs published in high-impact journals that regularly include cardiovascular studies.6 The aim was to explore the heterogeneity of the components of the primary CEPs of the RCTs eligible in the 3 domains mentioned above in the practical guidelines for interpretation: a) the importance (clinical significance); b) the frequency of events; and c) the size of the treatment effect.

To do this, a systematic review of studies published in general medicine and cardiology journals with greatest impact factor in 2003 was conducted using the MEDLINE database. Specifically, the Lancet, Annals of Internal Medicine, JAMA, New England Journal of Medicine, Circulation, and European Heart Journal were reviewed from January 1, 2002, through June 30, 2003. Journals covering the cardiovascular field but more centered on basic science were excluded (for example, Circulation Research). In addition, studies were excluded if a CEP was included but this was comprised solely of components related to the safety or toxicity of a drug or of paraclinical, or laboratory measures (surrogate outcomes). Likewise, group analyses that ignored random allocation were also excluded.

Two cardiologists and 9 internists with training in the methodology of clinical research and epidemiology independently classified the 72 outcome measures found to form part of the CEPs into 5 categories in decreasing order of "importance to the patient": 1 = death, 2 = critical, 3 = major, 4 = moderate, and 5 = minor. The group of investigators involved in the classification resolved any discrepancies by discussion until a consensus was reached for the classification.

A total of 242 potentially eligible RCTs were found. Of these, 114 met the inclusion criteria and formed the sample for analysis. In 41% of the studies, more than 1 CEP was used. The CEPs used were mostly comprised of 2 (34%) or 3 (39%) components; mortality was the most common component.

The study showed that outcomes of high clinical significance (such as mortality and other events classed as "critical") along with outcomes of less relative importance (category 4 or 5) were often included in the same CEP (57% of the studies). With regard to the heterogeneity of the effect of the intervention, in 75% of the cases it was observed that the effect of the intervention on the components differed moderately or substantially. The same could be said for the frequency of events of the components. Overall, only 14% of the CEPs analyzed were homogeneous in all 3 aspects.

It was also shown that both the effect of the intervention and the frequency of events were dominated more often than not by less important components and that the effect on the most important components was clinically insignificant. Table 3 shows how the both the frequency of events in the control group of the CEP as well as the size of the treatment effect increased markedly as CEP components of less clinical significance were added.

Finally, although the systematic review focussed only on the 6 journals of general medicine and cardiology with highest impact factor at the time, we should also point out that the use of CEP is common in Spain, and examples can be found in both randomized and observational studies.12

In brief, the use of potentially problematic CEPs in terms of interpretation is common in cardiovascular RCTs. The biggest risk of using these CEPs is that they exaggerate the real benefit of the intervention by expressing the outcome of the intervention in apparently plausible terms of greater clinical benefit. A reader of medical literature in general, and cardiology literature in particular, should be particularly cautious when interpreting the findings of RCTs expressed in the form of CEPs.

CONCLUSIONS

CEPs are often used as a methodological resource. The aim most often cited for their use is to increase the efficiency of the clinical trials when a small interventional effect is expected. They can also provide a measure of the net global effect of an intervention and, occasionally, be useful for avoiding a risk of bias due to competitive risks.

It is important to carefully assess the findings of the studies that use CEPs to avoid inappropriate interpretations.

When CEPs are used, the clinical significance of the effect is related to the degree of heterogeneity of the components in 3 domains: relative clinical significance, size of effect, and frequency of events. The higher the degree of heterogeneity in these domains, the greater the uncertainty about the clinical significance of the effect of the intervention.

In the current literature, it is common to use CEPs with a marked gradient of clinical significance among their components and in which the size of the effect of the intervention on the components of lesser importance predominates. These circumstances could favor an exaggeration of the real benefit of the interventions that they evaluate.

ABBREVIATIONS

AMI: acute myocardial infarction CEP: composite endpoint
RCT: randomized controlled trial RRR: relative risk reduction

Correspondence: Dr. G. Permanyer-Miralda.
Unidad de Epidemiología. Servicio de Cardiología. Hospital Vall d'Hebron. Pg. Vall d'Hebron, 119-129. 08035 Barcelona. España.
E-mail: gpermany@gmail.com